Já vimos em Conservação do Momento Linear que a origem do movimento de translação está ligada à origem de outro movimento. Mas será que esse fenômeno também está relacionado com o movimento de rotação?

Podemos pensar em algumas situações como, por exemplo, quando uma pessoa está em cima de uma esteira. Ela empurra a esteira para trás, a esteira começa a girar em sentido contrário ao da pessoa.

Resultado de imagem para pessoa andando na esteria gif Temos também um ratinho dentro de uma gaiola cilíndrica, fixa em um eixo, que permite ela girar livremente. Quando o ratinho começa a correr em um sentido a gaiola gira para outro.

Resultado de imagem para pessoa andando na esteria gif

Uma pessoa ao usar a furadeira deve segura – la com força, pois ao ser ligada tenta girar no sentido oposto ao da broca.

Imagem relacionada

Outra situação bem interessante é quando o início do movimento de rotação de um objeto origina o início do movimento de rotação de outro. Esse exemplo pode ser o de duas pessoas sentadas em cadeiras giratórias, em que ambas retiram os pés do chão e uma empurra a outra provocando uma rotação, em que o sentidos das rotações para os dois corpos serão opostos.

Essas situações mostram que a origem de um movimento de rotação está ligado a outro movimento de rotação em sentido oposto.

A origem de um movimento de rotação está sempre associada à origem de outro movimento de rotação em sentido oposto.

Pare entendermos essa origem de movimento devemos entender o que é torque.

Torque

Abrir uma porta, girar uma torneira, trocar o pneu de um carro, estão relacionados com o movimento de rotação.

Em ambos exemplos são aplicadas forças, no pneu a mão do homem segura a chave e aplica uma força para cima ou para baixo para torcer o parafuso; na torneira aplica – se forças em sentidos opostos, que fará com que a torneira seja aberta ou fechada. As forças podem fazer o corpo girar em torno do eixo, adquirindo assim movimento de rotação.

Se a força resultante sobre os corpos for nula o objeto poderá estar em equilíbrio estático ou dinâmico.

A rapidez do giro de um objeto em torno de um eixo é determinada pela razão entre a variação angular $\Delta\theta$ realizado por qualquer ponto do objeto pelo intervalo de tempo $\Delta t$ , chamada de velocidade angular $\omega$

Considerando que cada volta completa equivale a $2\pi$ radianos, temos que a velocidade angular pode ser expressa como:

$\omega=\frac{2\pi}{\Delta t}$

As rotações podem ocorrer nos dois sentidos: horário e anti – horário. Para determinar seu sentido usa-se a regra da mão direita .

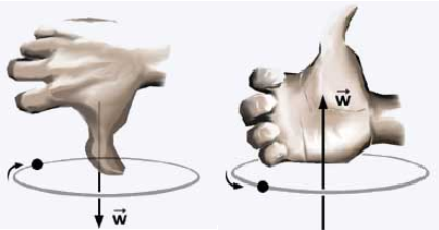
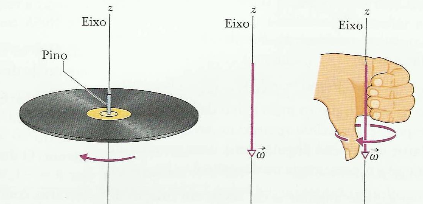
Em um disco girando, podemos identificar a direção da velocidade angular, posicionando o dedo polegar na direção do eixo de rotação e os demais dedos na direção da rotação.

A figura mostra um disco que gira no sentido anti – horário, aplicando a regra da mão direita, verifica-se que a direção da velocidade angular é vertical e sentido para baixo.

No movimento de rotação a velocidade linear não é constante, pois muda de direção e sentido, porém pode apresentar velocidade angular constante. Neste caso a velocidade angular sendo constante surge um novo conceito de equilíbrio, o torque.

Imagine que você irá abrir uma porta e pegar na maçaneta da porta, que está localizada o mais distante possível das dobradiças onde está localizado o eixo de rotação.

Agora imagine que você irá abrir a mesma porta só que agora a maçaneta está bem próxima da porta.

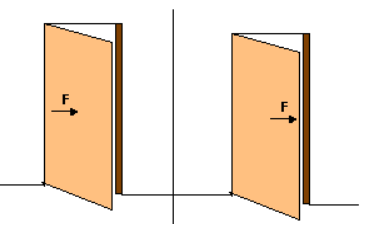Na primeira situação você certamente terá mais facilidade para abrir a porta, porém na segunda situação terá dificuldades, tendo que aplicar uma força maior para obter o mesmo resultado da situação anterior.

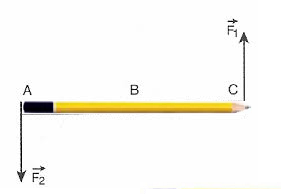
Agora observe a figura que representa uma caneta que sofre a ação de duas forças de mesma intensidade.

Certamente a caneta não girará, mas se as forças forem aplicadas perpendicularmente nas extremidades, ela girará.

O que provoca a rotação é chamado de torque ou momento de força

Para definir o torque, consideremos uma força $F$ aplicada a um ponto de um objeto conforme a figura.

O ponto $O$ representa a intersecção de um eixo perpendicular com o plano que contem os vetores $F$ e $r$ , sendo que o vetor $r$ situa o ponto de aplicação da força em relação a este eixo. Constrói – se a linha de ação desta força prolongando – se a reta ao longo da onde $F$ está. A distância perpendicular do eixo à reta de ação da força é $r=sen\theta$ onde $\theta$ é o ângulo entre as direções de $r$ e $F$

A expressão que determina o cálculo do torque $\tau$ é o produto da força $F$ perpendicular aplicada pela distância $d$ . A distância do pondo de aplicação da força ao eixo é chamado de braço de força. A unidade de medida no SI do torque é newton – metros (N.m)

$\tau =F_{\perp} d=rsen\theta F$

A direção do torque é dado pela regra da mão direita, perpendicular ao plano que contém contém r e F.

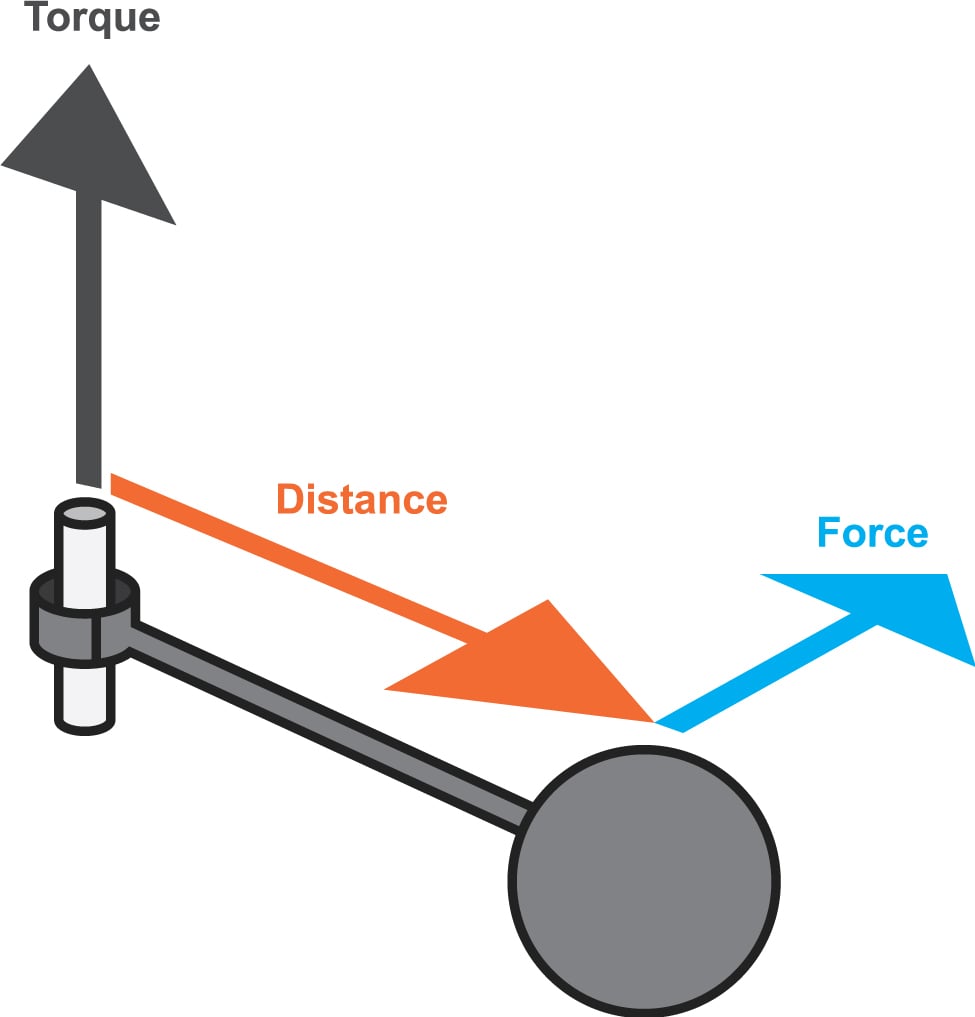
Resultado de imagem para torque

O módulo do torque em relação a um eixo é o produto do módulo da força pela distância perpendicular do eixo à linha de ação da força.

Voltando ao exemplo da porta agora podemos entender porque ao aplicar uma força mais distante do eixo de rotação teremos facilidade, pois de acordo com as equações podemos concluir que quando mais distante for o ponto de aplicação da força em relação ao eixo, menor será a força aplicada e o corpo terá mais facilidade para rotacional.

Em relação ao exemplo do lápis ele rotacional porque as forças perpendiculares aplicadas estão sentidos opostos, o que resultará em um torque resultante igual a zero, fazendo com que o lápis fique rotacionando.

Podemos verificar uma situação de equilíbrio no seguinte caso.

Imagine uma barra homogênea de comprimento 4 m e de peso P = 12 N está apoiada nos pontos A e B, conforme a figura.

Para que a barra permaneça em equilíbrio é necessário que a soma das forças exercidas pelos apoios A e B que tem direção vertical e sentido para cima seja igual a soma das forças que atuam sobre a barra na vertical e sentido para baixo para que a força resultante seja nula.

Na figura, a seguir, estão representadas as forças que agem na barra, as forças $F_{A}$ , $F_{B}$ e $P$ que representa a força peso. Como barra é homogênea o entro de massa da barra coincide com o centro de gravidade.Como queremos que a barra permaneça em equilíbrio temos que a resultante é nula e assim a barra não sofre movimento de translação. Então temos:

$F_{r}=ma\rightarrow F_{A}+F_{B}-P=0\rightarrow F_{A}+F_{B}=P (I)$

No entanto a barra pode sofrer movimento de rotação. Considerando o ponto B como referência temos que a força $F_{A}$ tende a girar a barra em torno de B, no sentido horário e o peso P tende a girar a barra em torno de B, no sentido anti-horário.Para que a barra não gire devemos impor que o torque de $F_{A}$ em torno de B (no sentido horário) deve ser igual ao troque de P em torno de B (no sentido anti-horário).

$\tau _{F_{A}}=\tau _{P}\rightarrow F_{A}d_{AB}=Pd_{PB}(II)$

Usando os dados da figura podemos calcular as forças $F_{A}$ e $F_{B}$

$F_{A}.3=12.1\rightarrow F_{A}=4N$

Usando a equação (I) temos que:

$F_{A}+F_{B}=P\rightarrow4+F_{B}=12\rightarrow F_{B}=8N$

Os módulos das forças e as distâncias $F_{A}$ , $F_{B}$ e $P$ e suas distâncias em relação ao referencial B garante nessas condições que a barra não irá girar. Porém se aproximarmos o referencial B (0,5m) de P temos que os torque gerados pelas forças $F_{A}$ e $P$ não serão mais os mesmos e a barra irá rotacional. Os valores dos torques seriam: $\tau _{F_{AB}}=4.2,5=10N$ e $\tau _{P_{AB}}=12.0,5=6N$

Resumindo: para o equilíbrio de um corpo extenso devemos impor:

1º) Equilíbrio de Translação:
Força resultante nula. Esta condição é imposta considerando a soma das intensidades das forças para cima igual à soma das intensidades das forças para baixo. E a soma das intensidades das forças para a direita igual à soma das intensidades das forças para a esquerda.

2º) Equilíbrio de rotação:
Neste caso, escolhemos um ponto e impomos que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário.

A segunda lei de Newton para a rotação

Vamos imaginar uma esfera fixa em uma haste girando em torno do eixo devido a aplicação de uma força $F$ .

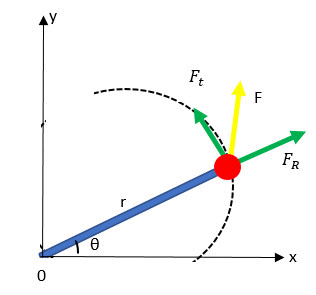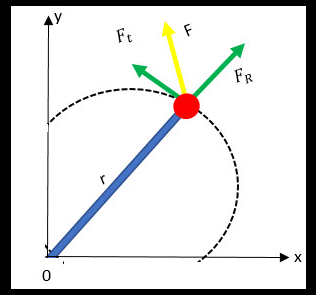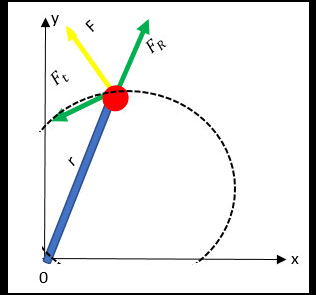
A componente tangencial $F_{f}$ com aceleração $a_{t}$ obedece a segunda lei de Newton:

$F_{t}=ma_{t}$

O torque que atua na partícula é $\tau =F_{t}r=ma_{t}r$ e que a aceleração tangencial é a aceleração de rotação $a_{t}=a_{r}r$ , podemos escrever o torque como:

$\tau =m(a_{r}r)r=(mr^2)a_{r}$

A grandeza entre parênteses é o momento de inércia da partícula em relação ao eixo de rotação. Então:

$\tau =Ia_{r}$

Caso exista mais de uma força aplicada sobre o corpo temos que a $\sum \tau =Ia_{r}$ medida em radianos.

onde $\sum$ é o torque resultante que atua sobre as partícula.

Resultado de imagem para golpe de judo gif

Para exemplificar vamos pensar em uma disputa de judô. Imagine que para atirar no solo um adversário de 80 kg, você utiliza o deslocamento em torno do quadril, um golpe em que tenta puxa-lo pelo uniforme com uma força F, que tem uma braço de alavanca $d_{1}=0,30m$ em relação ao ponto de apoio (eixo de rotação) no seu quadril direito, sobre o qual deseja girá -lo com uma aceleração angular de $-12rad//s^2$ , ou seja, uma aceleração no sentido horário e suponha que o momento de inércia é $15kgm^2$ .

a) Qual deve ser o módulo de F se, inicialmente você incliná -lo para frente, para fazer com que o centro de massa dele coincida com seu quadril?

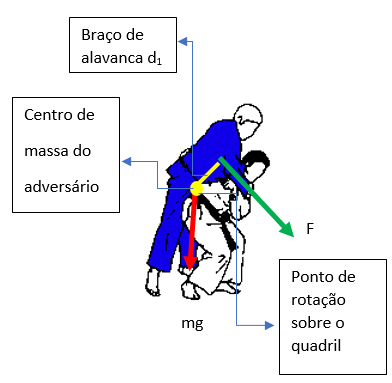
Resolução: Se o centro de massa dele estiver sobre o eixo de rotação, o vetor peso não produzirá torque em relação a esse eixo. Assim o único torque sobre ele é devido a sua força aplicada.

Considerando o torque no sentido horário negativo temos:

$\tau =-d_{1}F=Ia_{r}\rightarrow F=\frac{-Ia_{r}}{d_{1}}=\fra{-(15)(-12)}{0,30}=600N$

b) Qual será o módulo de F se o adversário permanecer ereto e o vetor peso dele tiver um braço de alavanca $d_{2}=0,12m$ em relação ao eixo de rotação?