Mecânica Lagrangeana

Uma outra forma de analisar a conservação da energia mecânica é considerando as propriedade de simetria e a mecânica Lagrangeana, na qual temos que a energia mecânica é definida por:

$E=K-V$

Imagine uma partícula que se move ao longo do eixo x em um campo potencial de energia potencial V(x).

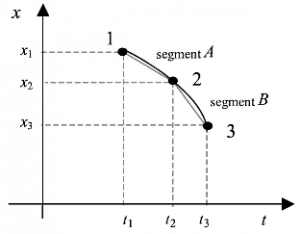
Considerando os segmentos A e B, o ponto 2 como ponto médio temos as seguintes variações de posições e seus respectivos intervalos de tempos.

$\Delta x_{A}=x_{2}-x_{1} , \Delta x_{B}=x_{3}-x_{2}$

$\Delta t_{A}=t_{2}-t_{1} , \Delta t_{B}=t_{3}-t_{2}$

A ação do segmento pode ser escrita por:

$S=\frac{1}{2}m\frac{({x_{2}-x_{1}})^{2}}{t_{2}-t_{1}}-V(\frac{x_{2}-x_{1}}{2}).(t_{2}-t_{1})$

A variação de tempo aprece na equação, portanto a ação é simétrica para um deslocamento fixo no tempo t. Escrevendo a ação como variação de espaço muitos pequenas em seus respectivos intervalos de tempos pequenos para segmento temos que para que ocorra simetria a variação da ação deve ser zero. Assim:

$\frac{ds}{dt}=\frac{d(S(A)+S(B))}{dt}=0$

$(\frac{1}{2}m\frac{{\Delta x_{A}}^{2}}{\Delta t_{A}}-V(\frac{x_{2}+x_{1}}{2})\Delta t_{A})\frac{1}{\Delta t_{A}}+(\frac{1}{2}m\frac{\Delta {x_{B}}^{2}}{\Delta t_{B}}-V(\frac{x_{3}+x_{2}}{2}\Delta t_{B})\frac{1}{\Delta t_{B}}$

$\frac{1}{2}m\frac{{\Delta x_{A}}^{2}}{\Delta {t_{A}}^{2}}+V(\frac{x_{2}+x_{1}}{2})=(\frac{1}{2}m\frac{\Delta {x_{B}}^{2}}{\Delta {t_{B}}^{2}}+V(\frac{x_{3}+x_{2}}{2})$

As expressões em ambos os lados da equação são somas de energia cinética e potenciais médias. Para eventos infinitamente infinitos, a equação dá uma igualdade para os valores instantâneos $\frac{1}{2}m{v_{A}}^{2}+V_{A}=\frac{1}{2}m{v_{B}}^{2}+V_{B}$ e expressa a conservação da energia mecânica. Em seguida, realizamos um argumento que traduz a multiplicação dos três instantes $t_{1}, t_{2}, t_{3}$ pela mesma quantidade e quando são derivados são tomados em relação ao tempo.

Mecânica Lagrangeana

Produto educacional do MNPEF – Polo UFABC