Forças Conservativas e Não-Conservativas
Considere uma força ![]() atuando sobre um corpo. A força é dita conservativa se o trabalho realizado por ela não depende do caminho percorrido, mas somente das posições inicial
atuando sobre um corpo. A força é dita conservativa se o trabalho realizado por ela não depende do caminho percorrido, mas somente das posições inicial ![]() e final do corpo
e final do corpo ![]() .
.
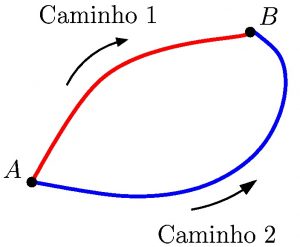
Para os caminhos 1 e 2 acima, temos
![]()
Se invertermos o sentido do caminho 2 percorrido, mantendo a mesma força, temos que o sinal do trabalho muda:
![]()
ou seja,
![]()
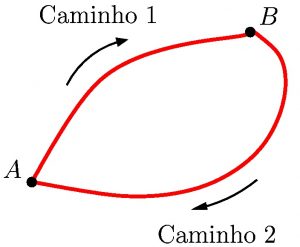
Mas a soma à direita representa o trabalho do percurso total, ida e volta. É um caminho fechado, onde o corpo parte de um ponto ![]() e chega num ponto
e chega num ponto ![]() através do caminho 1 e volta para
através do caminho 1 e volta para ![]() pelo caminho 2:
pelo caminho 2:
O resultado mostra que para uma força ser classificada como conservativa, o trabalho realizado por ela, sobre um corpo, é nulo para um caminho fechado (o corpo volta para o mesmo ponto de partida). A condição acima é necessária, mas não é o suficiente.
Vamos mostrar a seguir que o trabalho da força magnética, por exemplo,é nulo. No entanto, esta força é não-conservativa.
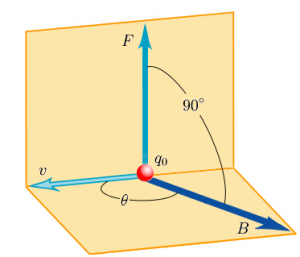
A força magnética surge quando um corpo carregado com carga se move em uma região com campo magnético. Se o corpo de carga elétrica ![]() e velocidade
e velocidade ![]() adentrar uma região do espaço com campo magnético
adentrar uma região do espaço com campo magnético ![]() , ele sentirá uma força magnética cuja intensidade é dada por
, ele sentirá uma força magnética cuja intensidade é dada por
![]()
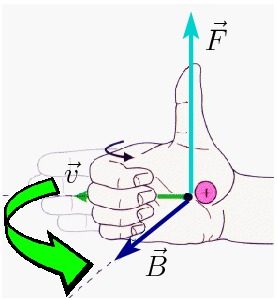
onde ![]() é o ângulo formado pelos vetores velocidade e campo magnético. A direção da força é perpendicular tanto à velocidade como ao campo magnético e o sentido é dado pela regra da mão direita, ilustrada na figura abaixo à direita; quatro dedos da mão direita fazem o movimento de
é o ângulo formado pelos vetores velocidade e campo magnético. A direção da força é perpendicular tanto à velocidade como ao campo magnético e o sentido é dado pela regra da mão direita, ilustrada na figura abaixo à direita; quatro dedos da mão direita fazem o movimento de ![]() para
para ![]() e o polegar dá a direção de
e o polegar dá a direção de ![]() .
.
Em notação vetorial mais avançada, a fórmula se resume a
![]()
onde ![]() denota o produto vetorial entre os vetores velocidade e campo magnético.
denota o produto vetorial entre os vetores velocidade e campo magnético.
Como a velocidade instantânea é paralela ao vetor deslocamento, temos que a força magnética atuando num corpo é sempre perpendicular ao seu deslocamento. Logo, como não haverá componente de ![]() na direção do movimento, temos a seguinte conclusão:
na direção do movimento, temos a seguinte conclusão:
Existe uma condição mais forte (necessária e suficiente) que uma força conservativa deve obedecer, mas a discussão envolve um conhecimento de Cálculo Vetorial, uma ferramenta imprescindível no estudo da Física e engenharia, mas bastante avançada para o nível deste site. Deixamos um link para curiosos ou quem quiser se aprofundar no assunto.

Trabalho de forças conservativas – exemplos
Como por definição o trabalho de forças conservativas não dependem de caminho, por simplicidade, vamos considerar uma trajetória unidimensional para os exemplos a seguir – o corpo se move em linha reta, a qual chamaremos de eixo ![]() . Neste caso, evidentemente o caminho de ida é igual ao caminho de volta.
. Neste caso, evidentemente o caminho de ida é igual ao caminho de volta.
Trabalho da força gravitacional (próximo à superfície da Terra)
Próximo à superfície da Terra, a força gravitacional (ou força peso) sobre um corpo de massa ![]() é dada por
é dada por ![]() , onde
, onde ![]() é o campo gravitacional produzido pela Terra. Próximo à sua superfície,
é o campo gravitacional produzido pela Terra. Próximo à sua superfície, ![]() possui valor constante aproximado de 9,8 m/s
possui valor constante aproximado de 9,8 m/s![]() . Se soltarmos qualquer objeto e desprezar a resistência do ar, ela cairá com aceleração de módulo igual a
. Se soltarmos qualquer objeto e desprezar a resistência do ar, ela cairá com aceleração de módulo igual a ![]() .
.
Vamos calcular o trabalho da força gravitacional sobre o corpo descendo uma rampa e mostrar explicitamente que ele não depende do comprimento da rampa, mas somente da altura ![]() da posição inicial
da posição inicial ![]() em relação à posição final
em relação à posição final ![]() , conforme mostra a figura abaixo:
, conforme mostra a figura abaixo:
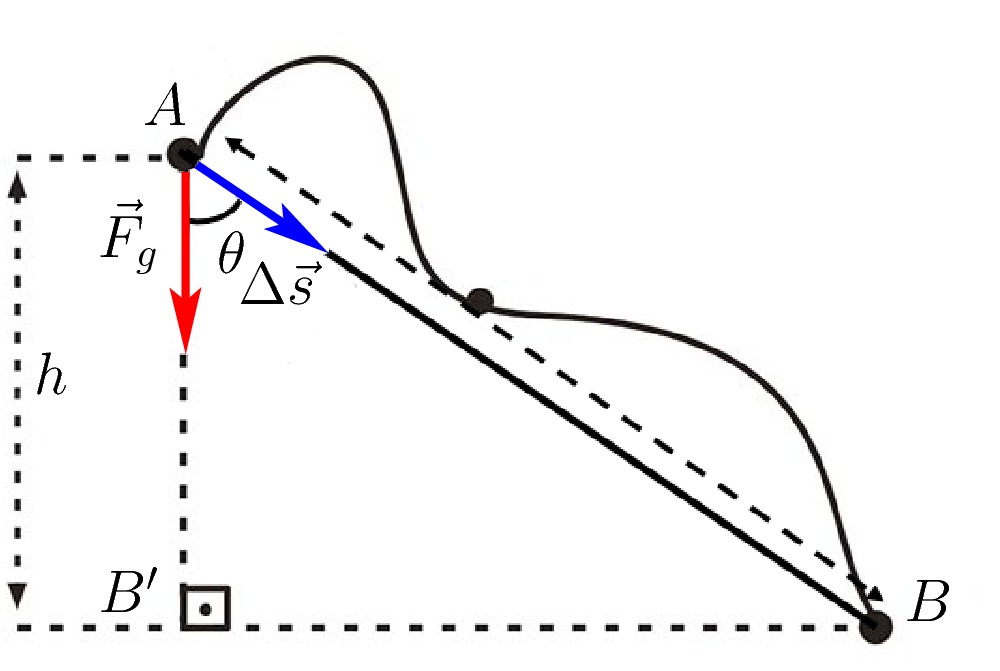
Conforme mostra a figura acima, a força gravitacional ![]() e o vetor deslocamento
e o vetor deslocamento ![]() formam um ângulo
formam um ângulo ![]() . A componente de
. A componente de ![]() na direção do deslocamento é
na direção do deslocamento é ![]() .
.
Como ![]() é constante ao longo da rampa, podemos usar a fórmula do trabalho para uma força constante:
é constante ao longo da rampa, podemos usar a fórmula do trabalho para uma força constante:
![]()
Por outro lado, a rampa forma a hipotenusa de um triângulo retângulo que tem a altura ![]() como sendo um dos seus catetos. Como
como sendo um dos seus catetos. Como ![]() é cateto adjacente em relação ao ângulo
é cateto adjacente em relação ao ângulo ![]() , temos que
, temos que
![]()
Substituindo ![]() na equação do trabalho, obtemos
na equação do trabalho, obtemos
![]()
Se ao invés de descer pela rampa, se o corpo fizer uma trajetória vertical de ![]() até
até ![]() e depois uma trajetória horizontal de
e depois uma trajetória horizontal de ![]() para
para ![]() , teremos
, teremos
![]()
onde o segundo termo é zero porque a força gravitacional é perpendicular ao deslocamento horizontal. Logo,
![]()
conforme esperado para uma força conservativa.
Podemos generalizar o resultado para qualquer caminho de ![]() para
para ![]() , como o caminho ondulado acima da rampa. Para isto, basta dividirmos a trajetória em pequenos trechos verticais e horizontais. Os trechos horizontais dão trabalho nulo e a soma dos trechos verticais dá
, como o caminho ondulado acima da rampa. Para isto, basta dividirmos a trajetória em pequenos trechos verticais e horizontais. Os trechos horizontais dão trabalho nulo e a soma dos trechos verticais dá ![]() .
.
Não é difícil mostrar que o trabalho de subida, de ![]() até
até ![]() é
é ![]() , de forma que o trabalho do trajeto fechado (descida + subida) é zero, como deveria ser.
, de forma que o trabalho do trajeto fechado (descida + subida) é zero, como deveria ser.
Trabalho da força gravitacional – caso geral
Próximo à superfície da Terra, um corpo de massa ![]() é atraído à Terra pela força gravitacional
é atraído à Terra pela força gravitacional ![]() . Esta força é um caso particular da força responsável pela atração entre corpos, postulada por Newton através da Lei da Gravitação Universal, a qual diz que
. Esta força é um caso particular da força responsável pela atração entre corpos, postulada por Newton através da Lei da Gravitação Universal, a qual diz que
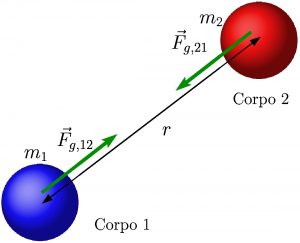
Como os corpos se atraem mutualmente, a força está na direção que conecta os seus centros de massa e o seu módulo é
![]()
onde ![]() e
e ![]() são as massas dos corpos,
são as massas dos corpos, ![]() é a distância que separa os seus centros de massa e
é a distância que separa os seus centros de massa e ![]() a constante gravitacional universal, cujo valor aceito atualmente é
a constante gravitacional universal, cujo valor aceito atualmente é
![]()
Como o próprio nome diz, essa constante é universal; não importa se trata da queda de uma maçã, um satélite que é mantido na órbita da Terra, a atração gravitacional que o Sol exerce sobre a Terra, etc.

A força de gravitação universal de Newton é uma das forças fundamentais da Natureza e obedece a terceira lei de Newton, ou seja,
![]()
Para calcular o trabalho realizado pela força gravitacional, vamos manter o corpo 1 fixo e deslocar somente o corpo 2. Inicialmente, estão separados por uma distância ![]() e após o deslocamento, passam a estar separados por uma distância
e após o deslocamento, passam a estar separados por uma distância ![]() , conforme mostra a figura abaixo.
, conforme mostra a figura abaixo.
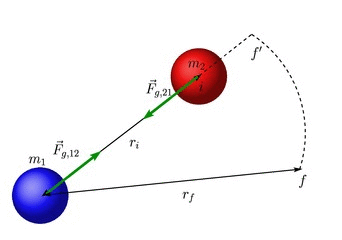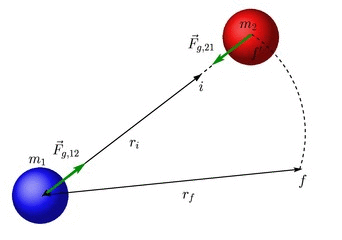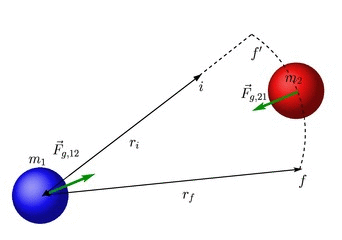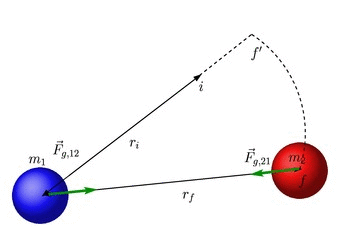
Como o trabalho da força gravitacional não depende do caminho, vamos escolher o caminho 2, constituido dos trechos ![]() e
e ![]() . No segundo trecho, a força é perpendicular ao deslocamento, portanto o trabalho não é nulo. Temos portanto que
. No segundo trecho, a força é perpendicular ao deslocamento, portanto o trabalho não é nulo. Temos portanto que
![]()
O sinal negativo na força é porque quando o corpo 2 vai se afastando (![]() aumenta), a força sobre ele aponta no sentido contrário ao do deslocamento.
aumenta), a força sobre ele aponta no sentido contrário ao do deslocamento.
Um curso introdutório de Cálculo é o suficiente para entender que ![]() . Substituindo os limites da integral,
. Substituindo os limites da integral,
![]()
Trabalho da força elástica
O trabalho da força elástica já foi calculada na página “Trabalho e Energia Cinética“. Iremos agora só mostrar que o trabalho dessa força respeita a condição necessária para o trabalho de uma força conservativa.
Recordando que a força elástica é dada por ![]() , o trabalho realizado por essa força atuando num corpo, de
, o trabalho realizado por essa força atuando num corpo, de ![]() até
até ![]() , é dado por
, é dado por
![]()
onde ![]() como
como ![]() podem ser tanto deformação quanto elongação da mola. Se fizermos a troca
podem ser tanto deformação quanto elongação da mola. Se fizermos a troca ![]() , temos que
, temos que ![]() e portanto o trabalho total ida e volta dá zero.
e portanto o trabalho total ida e volta dá zero.
A simulação a seguir permite verificar que para um percurso de ida e volta, as deformações são iguais e as contribuições de trabalho positivo e negativo se cancelam, pois tem a mesma intensidade mas sinais opostos devido ao sentido da deformação e da força.
Trabalho de força não conservativa – a força de atrito
Trabalho da força de atrito
A força de atrito cinético atuando sobre um corpo de massa ![]() deslizando sobre uma superfície rugosa é dada por
deslizando sobre uma superfície rugosa é dada por
![]()
onde ![]() é a força normal. Por simplicidade, vamos analisar o movimento do corpo andando em linha reta, horizontal à superfície da Terra. Neste caso,
é a força normal. Por simplicidade, vamos analisar o movimento do corpo andando em linha reta, horizontal à superfície da Terra. Neste caso, ![]() , e observamos que a força de atrito sempre tem o sentido contrário do movimento. A força
, e observamos que a força de atrito sempre tem o sentido contrário do movimento. A força ![]() puxando o bloco não influencia em nada o cálculo do trabalho da força de atrito.
puxando o bloco não influencia em nada o cálculo do trabalho da força de atrito.

Novamente, como o módulo da força de atrito é constante, o cálculo do trabalho é simples. Observa-se, no entanto, que o sentido da força de atrito é sempre contrário ao do deslocamento. Com isto,
![]()
Se o corpo percorrer uma distância ![]() entre as posições
entre as posições ![]() e
e ![]() , temos que
, temos que ![]() . Logo,
. Logo,
![]()
Temos portanto que








