O que é Momento Linear?

Nos livros do ensino médio, o que chamamos de momento linear é conhecido como quantidade de movimento.

No tópico Conservação de Energia, verificamos a importância em identificar as várias formas de energia. Em particular, nós temos a energia cinética de uma partícula, que é uma energia associada à velocidade da partícula. Se ela possui massa $m$ e velocidade $v$ , o momento linear é definido como sendo

$\vec{p} = m \vec{v}$

Momento linear de uma partícula é o produto entre a sua massa e o seu vetor velocidade.

Como $m$ é uma grandeza escalar e $\vec{v}$ uma grandeza vetorial, o produto deverá ser um vetor. Desta forma, o momento linear é uma grandeza vetorial; assim como a velocidade, força, etc., possui módulo, direção e sentido.

A unidade do momento linear no sistema internacional de unidades é kg $\cdot$ m/s.

Por que precisamos associar uma nova grandeza à uma partícula de massa $m$ e velocidade $\vec{v}$ ? Não seria suficiente conhecermos a sua posição, velocidade, força sobre ela (que determina a aceleração) e a energia cinética?

Veremos adiante que essa grandeza física torna-se imprescindível no entendimento de vários fenômenos físicos, como processos de colisão (clássica e de partículas), decaimento (como vimos na seção Relatividade e Equivalência Massa – Energia), movimento de foguete no espaço sideral, saque em um jogo de tênis, etc. Podemos listar uma infinidade de fenômenos observados no cotidiano em que o seu entendimento se dá através do momento linear.

Em algumas situações específicas, o momento linear se conserva. Ou seja, o momento linear permanece constante durante determinados processos.

Por que estudar o momento linear?

Vamos apresentar duas ações bastante corriqueiras do dia-a-dia.

A bola entra em movimento quando o jogador a chuta. Isto ocorre quando o pé em movimento entra em contato com a bola. Na linguagem popular (não científica), dizemos que quanto maior a força com que o jogador chuta, maior será a velocidade da bola.

Resultado de imagem para gif menino chutando a bola

É claro que no processo do chute, sentimos o contato do pé com a bola. Mais ainda, se o jogador se preparar para “encher o pé na bola” e a furar, ele pode sofrer uma contusão muito séria.

Vamos imaginar um outro esporte, o jogo de tênis, que também se utiliza uma bola. Ao invés dos pés, utiliza-se uma raquete para colocar a bola em movimento (no caso de um saque) ou para mudar a direção, sentido e/ou a intensidade da velocidade da bola.

Assim como no chute, apesar de se fazer o uso da raquete, quando a bola é rebatida pode-se sentir uma força sendo transferida para o braço.

Continuando com o tênis, nem sempre o objetivo é imprimir a maior velocidade na bola. Existe um outro fator, que é o ângulo com que a bola atinge a quadra. Numa deixadinha, por exemplo, isso fica bastante nítido. É a combinação entre a intensidade da velocidade e a sua direção que faz com que o adversário não consiga chegar na bola.

Existe um outro aspecto bastante importante na prática envolvendo esses dois esportes jogados com a bola: o efeito (ou o spin, na linguagem popular) que é dado na bola. Infelizmente, por envolver uma análise física bastante complexa, não entraremos em discussão nesse tipo de movimento.

Vamos analisar em maior detalhe o contato com a bola, o que a faz mudar de velocidade. O contato implica numa força aplicada sobre a bola. Essa força muda a direção, sentido e/ou a intensidade da velocidade da bola.

Após o contato com o pé ou com a raquete, essa força deixa de agir sobre a bola. Desprezando-se o efeito da resistência do ar, a única força agindo sobre a bola é a força gravitacional. Mas durante o processo do chute, a força gravitacional não é importante.

Existe uma outra variável importante que entra no processo do chute, saque ou rebatida da bola. O que ocorreria com a velocidade da bola após esse processo se a sua massa for muito diferente da usual? Certamente um atleta notaria a diferença imediatamente.

Temos portanto que força, velocidade e aceleração estão relacionados. Isto remete à segunda lei de Newton, a qual diz que $F = ma$ , onde $a$ é a aceleração do objeto de massa $m$ .

O que difere esse processo de contato é que a força que age sobre a bola possui uma pequena duração. Antes da batida e após a batida, se desprezarmos a resistência do ar e a força gravitacional, a partícula terá velocidade constante. Como a massa não muda nesse processo, podemos concluir que o seu momento linear também permanece constante.

Se considerarmos o momento linear do pé do atleta e da raquete do tênis, temos o momento linear do sistema. É possível que essa grandeza se conserve?

Para facilitar uma discussão mais técnica, podemos analisar o caso em que uma bola atinge uma superfície fixa (bola de tênis atingindo a quadra) ou uma bola atingindo uma outra bola, que é o processo conhecido como colisão em física.

Em ambas as situações, é fundamental o conceito de momento linear.

Uma terceira situação também é explicada em termos do momento linear: o movimento do foguete no espaço sideral. O foguete é construído com vários estágios; para ganhar velocidade, os estágios vão sendo desacoplados (jogados) . Além disto, mesmo construído com um único estágio, o foguete vai perdendo massa a medida que o combustível vai sendo queimado. O que isso tem a ver com o momento linear?

A seguir, vamos relacionar o momento linear com a força que age durante o processo de colisão.

Impulso e a Variação do Momento Linear

Para prosseguir a nossa discussão, vamos voltar ao exemplo da raquete. Quando a bola atinge a raquete, ela provoca um impacto na mesma porque possui momento. Esse impacto é sentido no braço que está segurando a raquete. Por outro lado, esse impacto também é responsável pela mudança na direção, sentido e talvez intensidade da bola. Logo, há uma variação do momento linear da bola.

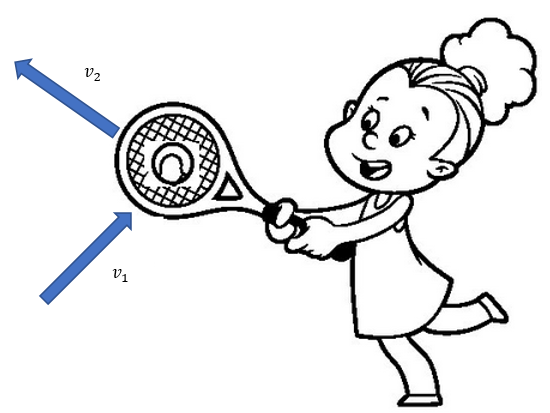
A variação de momento linear é analisada a partir da Segunda lei de Newton $\vec{F}=m\vec{a}$ . Se a velocidade muda, isso significa que existe uma aceleração $\vec{a}$ , visto que $\vec{a}_m=\frac{\Delta \vec{v}}{\Delta t}$ para a média em intervalo de tempo $\Delta t$ ou $\vec{a} = d\vec{v}/dt$ para a aceleração instantânea.

Antes de prosseguir, vamos enunciar a segunda lei de Newton na forma não muito conhecida no ensino médio.

A Segunda Lei de Newton

Qualquer aluno do ensino médio que já cursou Mecânica tem familiaridade com as leis de Newton. Em particular, aplicações da segunda lei são bastante exploradas em forma de exercícios acadêmicos de mais variadas formas, como plano inclinado, movimento de rotação, etc.

No ensino médio, a segunda lei costuma ser enunciado como

A força resultante que age sobre um corpo é igual ao produto da massa do corpo pela sua aceleração.

Em linguagem matemática,

$\vec{F_\textrm{res}} = m \vec{a}$

onde $\vec{F_\textrm{res}} = \vec{F}_1 + \vec{F_2} +\ldots$ é a força resultante que age sobre o corpo de massa $m$ .

Vale observar que a expressão só é válida em referenciais inerciais. O que são referenciais inerciais? A primeira lei de Newton justamente define o que é um referencial inercial.

Uma forma mais geral de enunciar a segunda lei de Newton (considerada a forma original) é

A taxa de mudança do momento de um corpo é diretamente proporcional à força aplicada sobre o mesmo.

Matematicamente,

$\vec{F} = \frac{d\vec{p}}{dt}$

Observa-se que para o caso em que a massa do corpo não muda durante a aplicação dessa força ( $m$ constante), tem-se que

$\vec{F} = \frac{md\vec{v}}{dt} = m \frac{d\vec{v}}{dt} = m\vec{a}$$

ou seja, recuperamos a forma mais conhecida da segunda lei de Newton.

A segunda lei, enunciada dessa forma, embasa a nossa discussão da variação do momento na presença de uma força.

A interação da raquete ou do pé com a bola possui duração muito pequena. Vamos considerar por ora que a força agindo num intervalo $\Delta t$ seja constante, que implica que a aceleração é constante, pois a massa da bola não muda. A segunda lei de Newton fica:

$\vec{F}=m\frac{\vec{v}_{2}-\vec{v}_{1}}{\Delta t} \quad \Rightarrow \quad \vec{F} \Delta t =m\vec{v}_2-m\vec{v}_1 = \Delta \vec{p}$

O lado esquerdo da última equação apresenta a força aplicada no objeto multiplicada pelo intervalo de tempo. Essa grandeza é chamada impulso, $\vec{I}$ , que corresponde à variação do momento linear: $\vec{I} = \Delta \vec{p}$ . Logo,

Impulso é a variação do momento linear, é força multiplicada pelo intervalo de tempo.

Matematicamente,

$\vec{I} = \Delta \vec{p} = \vec{F} \Delta t$

Essa força, que atua somente durante o contato com a raquete, é chamada de força impulsiva. É uma força muito intensa que existe apenas por um intervalo de tempo muito pequeno.

A figura abaixo mostra que pela distorção da bola e da raquete, a força (impulsiva) exercida pela raquete sobre a bola é de grande intensidade.

Resultado de imagem para gif bola de tenis atingida por uma raquete

Em módulo, temos que:

$I = F \Delta t$

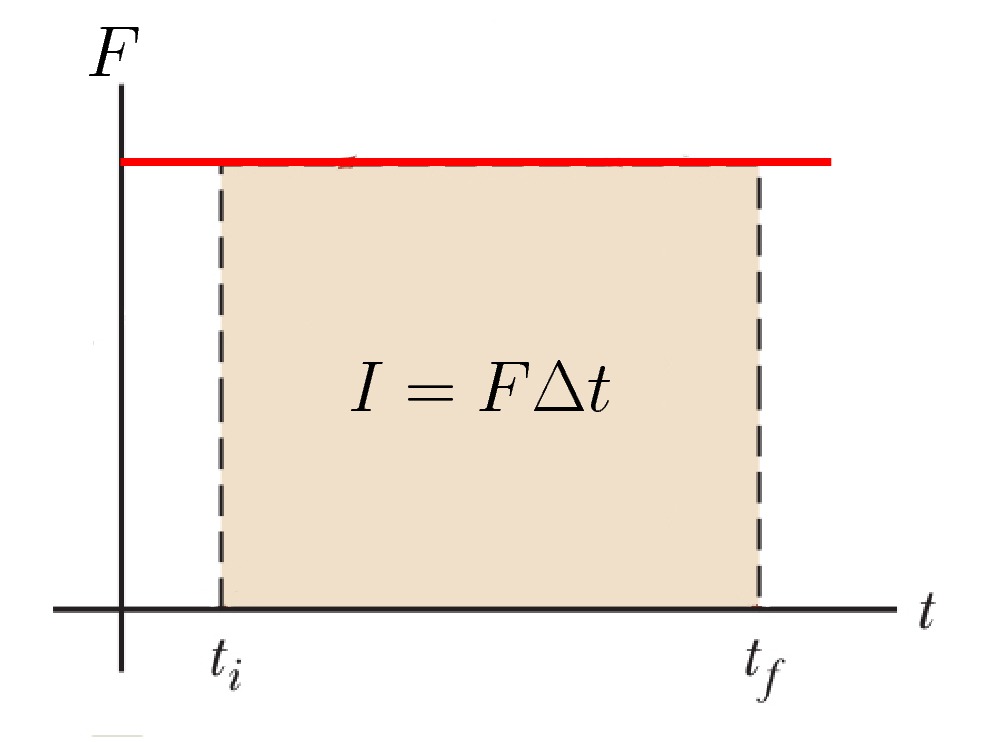
Se fizermos um gráfico de força versus tempo, o módulo do impulso é pela área sob a curva do gráfico, conforme mostra a figura abaixo. A área do retângulo corresponde numericamente a $F\Delta t$ , que é o módulo do impulso.

Quando a força não for constante, é difícil determinar experimentalmente como a força varia com o tempo, ou seja, $F(t)$ . Nesta situação, podemos considerar uma força impulsiva média, que é tratada como se fosse constante, como mostra a figura.

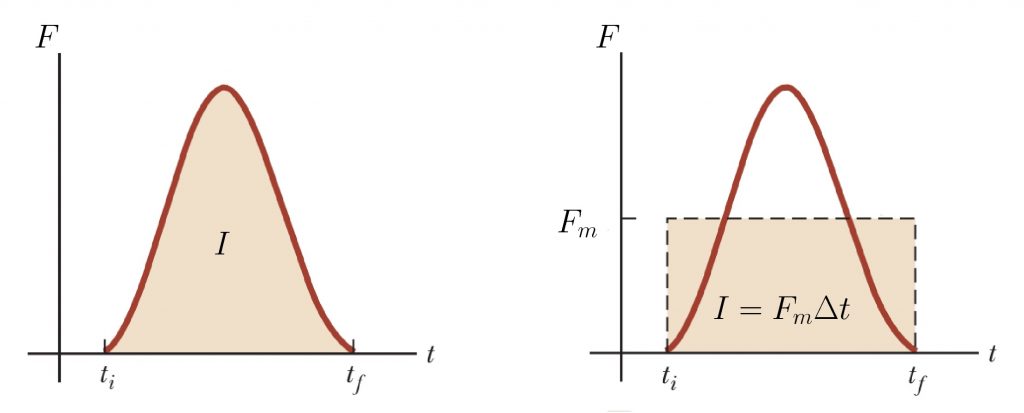
O valor médio de $F$ , $F_m$ , é tal que a área do retângulo na figura acima à direita é a mesma que a área sob a curva da figura à esquerda. Logo,

$I = \Delta p=p_{f}-p_{i}=\int_{t_{i}}^{t_{f}}Fdt = F_m \Delta t$

A equação mostra que o impulso é igual a variação do momento linear (da quantidade de movimento).

O impulso de uma força exercida sobre um objeto durante um intervalo de tempo $\Delta t$ é igual a variação de momento linear do objeto durante aquele intervalo de tempo.

Ação e Reação

O instante em que a bola entra em contato com a raquete, seu momento muda. É essa força que é sentida pelo braço.

Enquanto a bola está sendo atingida pela raquete existem outras forças atuando sobre ela, como a força gravitacional da Terra e a força exercida pelo ar. Porém, durante a ação da raquete essas forças são desprezíveis, sendo a força da raquete a única força relevante na alteração de movimento da bola.

Afinal, porque sentimos o “tranco” no braço? De onde vem essa força? Trata-se da força de reação, que é sentida pelo braço. As duas forças formam um par de forças do tipo ação e reação, explicado pela 3ª lei de Newton:

Quando um corpo exerce uma força sobre um segundo corpo, este exerce simultaneamente sobre o primeiro corpo uma força de mesma direção e intensidade, mas em sentido oposto.

Para ilustrar melhor esse par de forças, imagine dois patinadores parados, um próximo ao outro e de repente um deles empurra o outro. Essas forças podem ser consideradas forças impulsivas, os tipos que estamos considerando aqui. O que acontece é que os dois entram em movimento em sentidos opostos.

Resultado de imagem para gif patinação

O patinador, ao aplicar uma força $\vec{F}_{1(2)}$ sobre a patinadora, sente uma força $\vec{F}_{2(1)}$ , aplicada pela patinadora sobre ele.

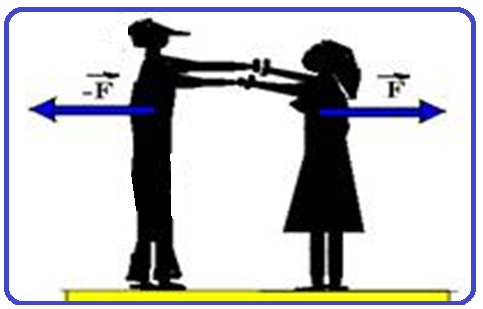
Temos portanto que a força resultante sobre o sistema (formado pelos dois patinadores) é zero:

$\vec{F}_{1(2)} + \vec{F}_{2(1)} = 0$

pois trata-se de forças do tipo ação – reação. Pela segunda lei de Newton, isto implica que

$\frac{d\vec{p_{1}}}{dt} + \frac{d\vec{p}_{2}}{dt}=0$

onde $p_1$ e $p_2$ são, respectivamente, os momentos do patinador e da patinadora.

Utilizando uma propriedade básica de derivada, que diz que a derivada da soma de duas funções é a derivada da soma, temos que

$\frac{d}{dt}(\vec{p}_1+ \vec{p}_2) = 0$

Essa equação diz que a derivada temporal ( $d/dt$ ) agindo sobre $\vec{p}_1+\vec{p}_2$ é zero. Isto significa que essa grandeza é uma constante em relação ao tempo, ou seja, não muda com relação ao tempo. Dizemos então que ela é uma grandeza conservada.