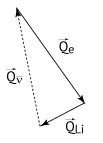
Objetos Extensos em Movimento de Rotação
Na seção anterior, discutimos a conservação do momento angular em diversas situações. Em todas elas, o sistema envolvia a rotação de objetos/corpos extensos, como uma bailarina rodopiando, um homem girando sentado na cadeira e segurando uma roda de bicicleta, etc.
Em todos eles, nós conseguimos compreender os fenômenos envolvidos, de forma qualitativa, à luz da lei da conservação do momento angular. Em nenhum momento questionamos qual deveria ser a velocidade da bailarina quando recua os membros. Só dizemos que a sua velocidade de rotação aumenta.
Se queremos fazer uma análise quantitativa, é fato que precisamos determinar o momento de inércia de um corpo extenso.
Sabemos que para uma partícula de massa 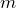 executando um movimento circular de raio
executando um movimento circular de raio  em torno de um eixo fixo é
em torno de um eixo fixo é
![Rendered by QuickLaTeX.com \[ I = m r^2 \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-249d7cf02594d11711827ca935a74ff2_l3.png)
Considere agora a rotação de um objeto extenso formado por 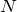 partículas, de massa
partículas, de massa 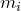 cada. Se o objeto é rígido, obviamente as massas estão fixas entre si, assim como as distâncias
cada. Se o objeto é rígido, obviamente as massas estão fixas entre si, assim como as distâncias 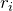 ‘s até o eixo de rotação.
‘s até o eixo de rotação.
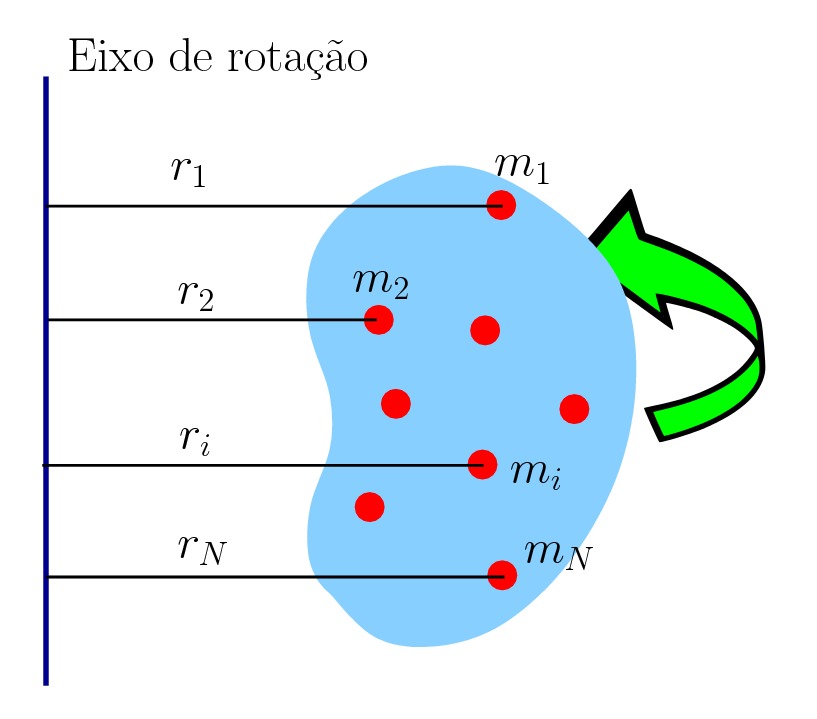
Neste caso, o momento de inércia do objeto é simplesmente a soma dos momentos de inércia de cada partícula
![Rendered by QuickLaTeX.com \[ I = \sum_i^N m_i r_i^2 \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-2720604a91547451431450e941b44ac4_l3.png)
A adaptação para um objeto extenso e contínuo segue imediatamente da expressão acima. Deixamos o link abaixo para quem tiver o interesse em calcular o momento de inércia para esse tipo de objeto.
Escrevemos acima a expressão para o momento de inércia de um corpo extenso granular. Caso o corpo seja contínuo, podemos imaginá-lo como sendo formado por partes muito pequenas de massa, cada uma com massa 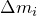 tendendo a zero. Assim,
tendendo a zero. Assim,
![Rendered by QuickLaTeX.com \[ I=\lim_{\Delta m_{i} \rightarrow 0} \sum {r_{i}}^{2}\Delta m_{i} \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-2ff7927e00fda882300288bdf557e18f_l3.png)
Na linguagem do cálculo, a somatória de coisas infinitesimais torna-se uma integral:
![Rendered by QuickLaTeX.com \[ I = \int r^2 dm \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-40483d610014f391f9933cece4cd00ba_l3.png)
A expressão acima é formal. Na prática, teremos de conhecer como a massa se distribui num objeto. Se ele for maciço tridimensional, devemos conhecer a sua densidade volumétrica de massa, 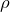 , que é massa por volume. Se a distribuição de massa não for homogênea, temos que
, que é massa por volume. Se a distribuição de massa não for homogênea, temos que
![Rendered by QuickLaTeX.com \[ \rho = \frac{dm}{dV} \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-09474350d1ac07f9862dbfc0c378046a_l3.png)
Logo, o momento de inércia será dado por
![Rendered by QuickLaTeX.com \[ I = \int_\textrm{volume} \rho r^2 dV \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-fdaa6581f17e875ed36103d27dfdf877_l3.png)
Para ilustrar como a fórmula acima funciona, vamos considerar um objeto mais simples; uma barra muito fina de comprimento 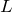 e massa m.
e massa m.
Neste caso, a distribuição da massa se dá ao longo do objeto e portanto temos uma densidade linear de massa, 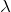 , onde
, onde
![Rendered by QuickLaTeX.com \[ \lambda = \frac{dm}{d\ell} \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-cdc12820c89c11f85f322567acce9cde_l3.png)
O momento de inércia fica, portanto,
![Rendered by QuickLaTeX.com \[ I = \int \lambda r^2 d\ell \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-c9e0066e74fa9df6596d038553a233b4_l3.png)
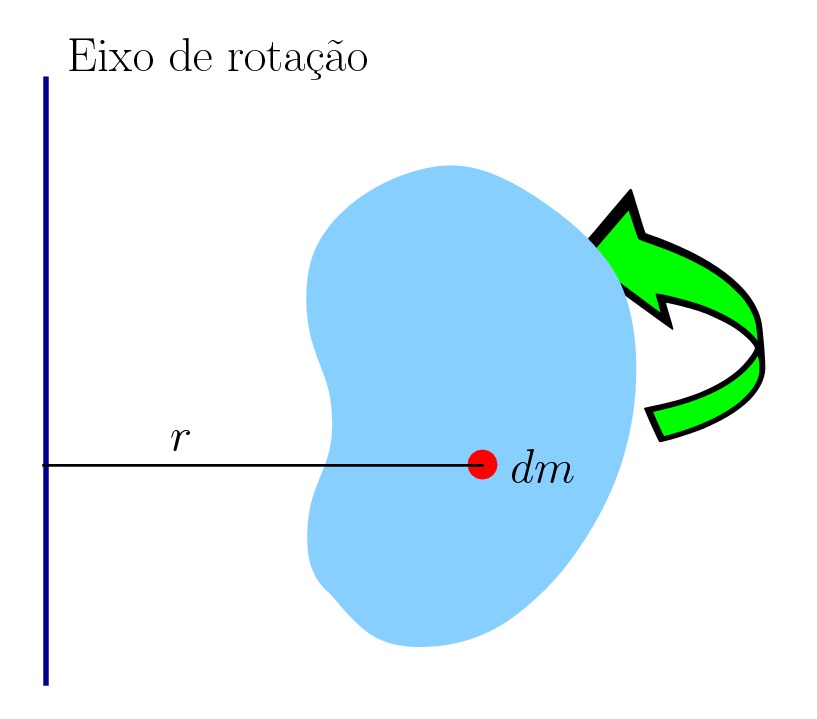
Vamos calcular o momento de inércia em relação a um eixo perpendicular à barra, que passa pelo centro de massa. Além disto, vamos assumir que a distribuição de massa é uniforme, ou seja, 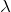 é constante, dada por
é constante, dada por
![Rendered by QuickLaTeX.com \[ \lambda = \frac{m}{L} \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-656d4e8805a2dafca003bb2998494a91_l3.png)
Vamos colocar a barra sobre o eixo 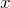 , com o seu centro de massa coincidindo com a origem
, com o seu centro de massa coincidindo com a origem  desse eixo. Para calcular o momento de inércia em relação ao eixo que passa pelo centro de massa e é perpendicular ao plano da tela, temos que
desse eixo. Para calcular o momento de inércia em relação ao eixo que passa pelo centro de massa e é perpendicular ao plano da tela, temos que 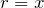 é a distância do elemento de massa
é a distância do elemento de massa 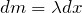 até o eixo.
até o eixo.

Temos que
![Rendered by QuickLaTeX.com \[ I_{cm} = 2 \lambda \int_0^{L/2} x^2 \; dx \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-e6c5c4b0cd9f02cad015a8dedcb39be3_l3.png)
O fator 2 surge porque tem o pedaço da barra à esquerda do eixo de rotação, que se estende de 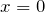 até
até 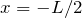 .
.
A integral dá 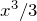 . Substituindo os limites e o valor de
. Substituindo os limites e o valor de 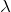 , obtemos
, obtemos
![Rendered by QuickLaTeX.com \[ I_{cm} = \frac{1}{12} m L^2 \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-69ebd053ab331c8a646afb518b53b29e_l3.png)
Se a mesma barra girar em torno de um eixo, também perpendicular a ela e que passa por um das extremidades, o momento de inércia será
![Rendered by QuickLaTeX.com \[ I = \int_0^L \lambda x^2 dx = \lambda \frac{x^3}{3}\bigg|_0^L \quad \Rightarrow \quad I = \frac{1}{3} mL^2 \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-2153bbb0f528ae6bc1ffd55477434c03_l3.png)
O link abaixo fornece o momento de inércia para vários formatos de objetos.
 Momento de inércia de vários objetos
Momento de inércia de vários objetos
Uma coisa importante para se observar é que o valor do momento de inércia depende do eixo o qual o objeto está girando. De fato, a partir da definição do momento de inércia, dá para se concluir qualitativamente que quanto maior a distância das massas em relação ao eixo de rotação, maior é o momento de inércia. É o que ocorre, por exemplo, quando seguramos os halteres com os braços abertos, que é maior do que quando fechamos os braços.
Por exemplo, o momento de inércia de uma barra fina de massa 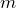 e comprimento
e comprimento 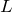 é
é 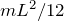 em relação ao eixo de rotação que passa pelo centro de massa da barra e é perpendicular a ela. Se o eixo estiver localizado numa extremidade da barra e continuar perpendicular a ela, o momento de inércia passa a ser
em relação ao eixo de rotação que passa pelo centro de massa da barra e é perpendicular a ela. Se o eixo estiver localizado numa extremidade da barra e continuar perpendicular a ela, o momento de inércia passa a ser 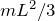 .
.
Observamos que
![Rendered by QuickLaTeX.com \[ I = I_{cm} + m L^2 \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-b8e1f58cf8fe99849e411aeef3aa7aa6_l3.png)
onde 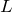 no segundo termo à direita corresponde, além do comprimento da barra, à distância entre os eixos. Veremos que esse resultado é geral, dado pelo teorema dos eixos paralelos, o qual afirma que
no segundo termo à direita corresponde, além do comprimento da barra, à distância entre os eixos. Veremos que esse resultado é geral, dado pelo teorema dos eixos paralelos, o qual afirma que
O momento de inércia de um corpo em relação a um eixo qualquer paralelo ao eixo principal, que passa pelo centro de massa do objeto, é igual à soma do momento de inércia em relação a esse eixo principal, dado por 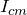 , com
, com 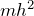 , onde
, onde 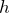 é a distância entre os eixos.
é a distância entre os eixos.
Logo,
![Rendered by QuickLaTeX.com \[ I = I_{cm} + mh^2 \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-b06653d3f969b38d0034e245414537cb_l3.png)
A figura abaixo mostra uma situação onde o teorema dos eixos paralelos pode ser aplicado.
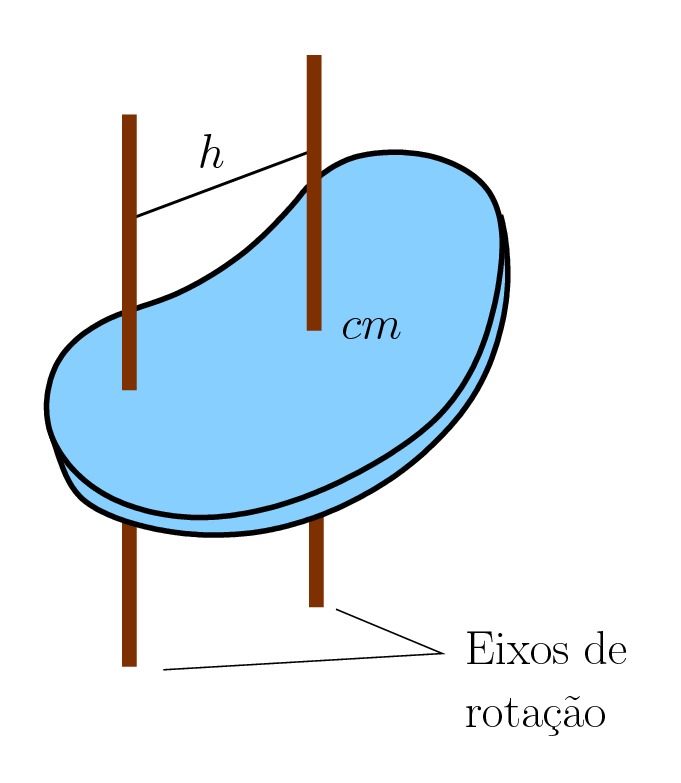
Caso queira saber como se demonstra o teorema dos eixos paralelos, clique no link abaixo.
Seja o ponto  a origem do sistema de coordenadas cartesianas, onde se localiza o centro de massa de um corpo de forma arbitrária. Considere o eixo
a origem do sistema de coordenadas cartesianas, onde se localiza o centro de massa de um corpo de forma arbitrária. Considere o eixo  como sendo um eixo de rotação e um outro eixo, paralelo a este, passando pelo ponto
como sendo um eixo de rotação e um outro eixo, paralelo a este, passando pelo ponto 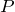 , caracterizado pelas coordenadas
, caracterizado pelas coordenadas 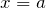 e
e 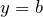 . Temos que a distância entre esses dois eixos paralelos é
. Temos que a distância entre esses dois eixos paralelos é 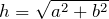 .
.
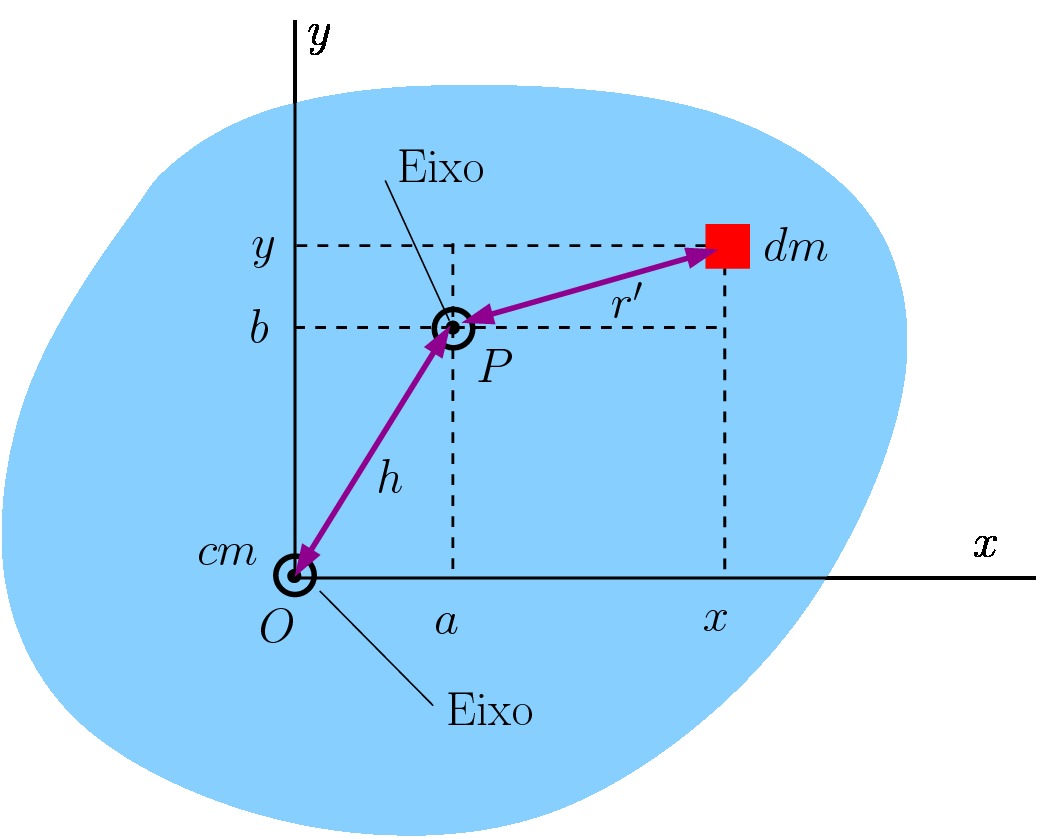
Considere um elemento de massa 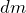 do objeto que se encontra na posição dada pelas coordenadas
do objeto que se encontra na posição dada pelas coordenadas 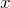 e
e 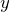 . Em relação ao ponto
. Em relação ao ponto 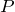 , a distância é
, a distância é
![Rendered by QuickLaTeX.com \[ r^\prime = \sqrt{(x-a)^2 + (y-b)^2} \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-6f630fda0d6c7db9f5fc4bee0443d746_l3.png)
O momento de inércia em relação ao ponto 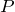 é dado por
é dado por
![Rendered by QuickLaTeX.com \[ I=\int r^{\prime 2}dm=\int \left [ \left ( x-a \right )^2+\left ( y-b\right )^2 \right ]dm \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-6a0e9da01e5ad738a14deedf5357496b_l3.png)
Abrindo os termos ao quadrado e lembrando que a integral da soma é a soma das integrais, temos
![Rendered by QuickLaTeX.com \[ I=\int \left ( x^2+y^2\right )dm-2a\int xdm-2b\int ydm+\left ( a^2+b^2 \right ) \int dm \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-437d9d799bd61ac5547e2ab6726df3db_l3.png)
A primeira integral acima é o centro de massa em relação ao centro de massa (que está na origem do sistema de coordenadas).
Já o segundo termo e o terceiro representam, respectivamente, a posição 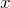 do centro de massa e a posição
do centro de massa e a posição 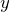 multiplicadas pela massa total veja a seção que discutimos o centro de massa . Como o centro de massa está na origem, temos que
multiplicadas pela massa total veja a seção que discutimos o centro de massa . Como o centro de massa está na origem, temos que 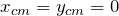 .
.
O último termo possui o termo 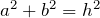 multiplicado pela integral, que dá a massa total do sistema.
multiplicado pela integral, que dá a massa total do sistema.
Logo, mostramos que
![Rendered by QuickLaTeX.com \[ I = I_{cm} + m h^2 \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-f3ccc64d3168e85509502b90ddc9bb8f_l3.png)
Vídeo: Momento de inércia
Ir para a próxima seção O Momento Angular e a Sua Conservação
![]() executando um movimento circular de raio
executando um movimento circular de raio ![]() em torno de um eixo fixo é
em torno de um eixo fixo é![]()
![]() partículas, de massa
partículas, de massa ![]() cada. Se o objeto é rígido, obviamente as massas estão fixas entre si, assim como as distâncias
cada. Se o objeto é rígido, obviamente as massas estão fixas entre si, assim como as distâncias ![]() ‘s até o eixo de rotação.
‘s até o eixo de rotação.
![Rendered by QuickLaTeX.com \[ I = \sum_i^N m_i r_i^2 \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-2720604a91547451431450e941b44ac4_l3.png)
 Momento de inércia de vários objetos
Momento de inércia de vários objetos ![]() e comprimento
e comprimento ![]() é
é ![]() em relação ao eixo de rotação que passa pelo centro de massa da barra e é perpendicular a ela. Se o eixo estiver localizado numa extremidade da barra e continuar perpendicular a ela, o momento de inércia passa a ser
em relação ao eixo de rotação que passa pelo centro de massa da barra e é perpendicular a ela. Se o eixo estiver localizado numa extremidade da barra e continuar perpendicular a ela, o momento de inércia passa a ser ![]() .
.![]()
![]() no segundo termo à direita corresponde, além do comprimento da barra, à distância entre os eixos. Veremos que esse resultado é geral, dado pelo teorema dos eixos paralelos, o qual afirma que
no segundo termo à direita corresponde, além do comprimento da barra, à distância entre os eixos. Veremos que esse resultado é geral, dado pelo teorema dos eixos paralelos, o qual afirma que![]()




![Rendered by QuickLaTeX.com \[ I = \int_0^L \lambda x^2 dx = \lambda \frac{x^3}{3}\bigg|_0^L \quad \Rightarrow \quad I = \frac{1}{3} mL^2 \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-2153bbb0f528ae6bc1ffd55477434c03_l3.png)