As leis de Newton possibilitam a compreensão dos comportamentos dinâmicos e estáticos de corpos que estão isolados ou interagindo com outros, que são observados em referenciais inerciais.
O referencial inercial é um sistema em que corpos livres não tem seu estado de movimento alterado, ou seja, corpo livres não sofrem acelerações, quando não há forças exercidas sobre eles.
A interação entre dois ou mais corpos é medida a partir do conceito de força, quantificando e analisando o resultado físico da interação sobre cada corpo, isto é, a interação entre pares de corpos, que são responsáveis pela mudança de velocidade dos corpos nos quais atuam.
1ª Lei de Newton – Princípio da Inércia
Isto significa que um objeto em repouso ou movimento retilíneo uniforme tende a permanecer nesse estado se a força resultante sobre ele é nula.
O princípio da inércia pode ser observado em várias situações como:
- No movimento de um ônibus, como mostra a simulação a seguir. Quando o ônibus “arranca” a partir do repouso, os passageiros tendem a deslocar-se para trás. Da mesma forma, quando o ônibus já em movimento freia, os passageiros deslocam-se para a frente, tendendo a continuar com a velocidade que possuíam.

- Um passageiro que pode ser arremessado para fora do carro, pois ele tende a continuar em movimento, já que a força externa aplicada pelo muro age sobre o carro e não sobre ele.

- O corpo tende a permanecer em repouso

A primeira lei é primordial para se estabelecer um referencial inercial, sistemas de referências em que corpos livres não tem o seu estado de movimento alterado, ou seja, corpos livres não sofrem acelerações quando não há forças sendo exercidas, pois as leis de Newton são válidas apenas para referenciais inerciais.
2ª Lei de Newton – Princípio Fundamental da Dinâmica
Uma das implicações da 1ª Lei de Newton é que para a velocidade de um corpo sofrer variação em um referencial inercial, ou seja, sofrer aceleração é necessário aplicação de força.
O estado de inércia de repouso ou movimento de um corpo depende de sua massa. Podemos comparar corpos com massas diferentes, como por exemplo, na situação a seguir.
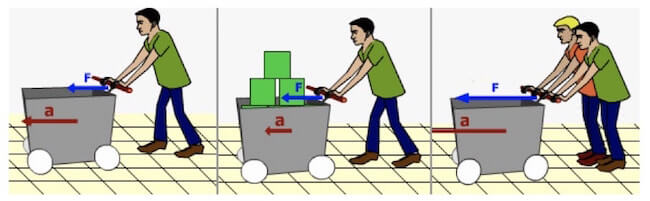
Na primeira e segunda situação verificamos pelo tamanho do vetor força, que a força aplicada é a mesma, porém a massa do corpo sobre qual a força atua foi aumentada e consequentemente a aceleração diminuiu. Comparando a primeira situação com a terceira a massa do corpo foi mantida constante, porém a intensidade da força aplicada aumentou e consequentemente a aceleração também aumentou.
Assim podemos afirmar que a relação entre a aceleração e a massa inercial de um corpo são grandezas inversas.
Escrevendo a força em função da aceleração temos a 2ª Lei de Newton – Princípio Fundamental da Dinâmica:
onde m é o coeficiente de inércia, isto é, a massa, associado ao corpo sobre o qual a força age.
Considerando que várias forças podem agir ao mesmo tempo sobre um corpo temos que a força resultante é a soma de todas as forças.
Vídeo : O vídeo explica a operação de vetores algebricamente e geometricamente.
No entanto, Newton não definiu sua segunda lei como: força é igual a massa vezes a aceleração, sua formulação original foi definida como “quantidade de movimento” em outras palavras “momento linear”. A definição é:
Isto significa que o momento linear de um corpo é:
Como m não varia com o tempo e fazendo a derivada em ambos membros da equação temos a formulação da 2ª Lei de Newton.
A equação mostra que o momento é proporcional à força aplicada, isto é, é a taxa de variação temporal da quantidade de movimento.
Podemos verificar a aplicação da 2ª Lei de Newton em algumas situações como:
- Plano Inclinado
Na figura observamos que as forças que atuam sobre o corpo são a força peso, devido a atração gravitacional da Terra e a força normal que é a força de reação da superfície, não há atrito.
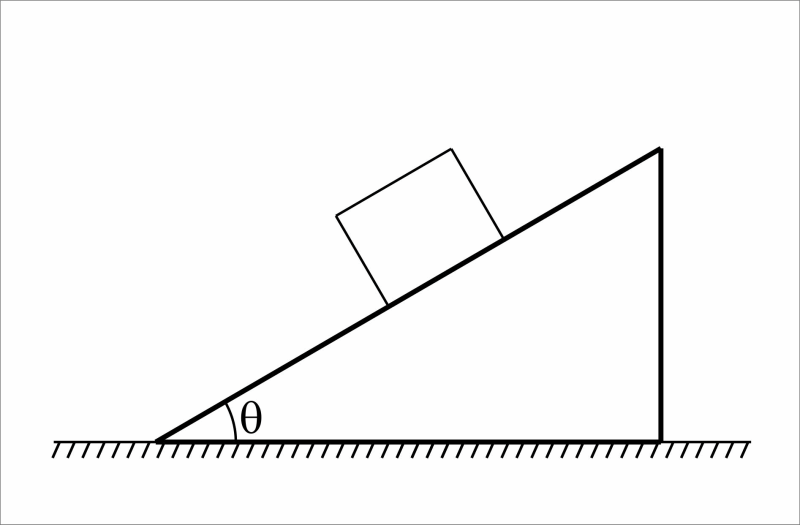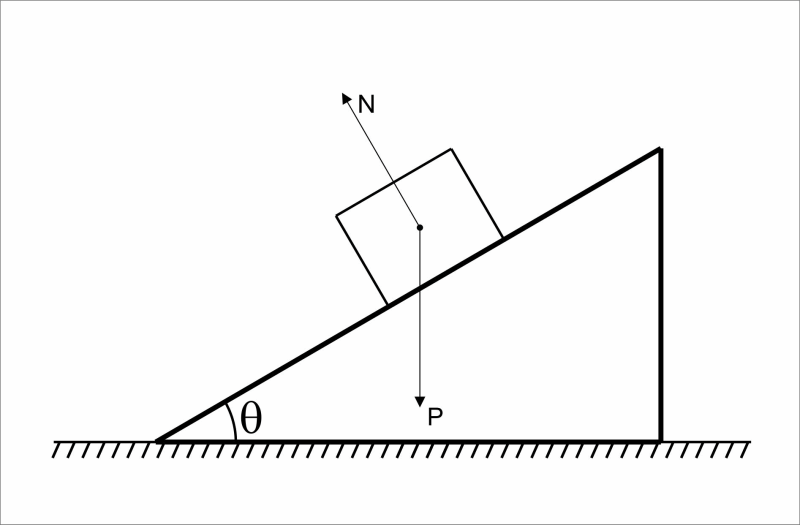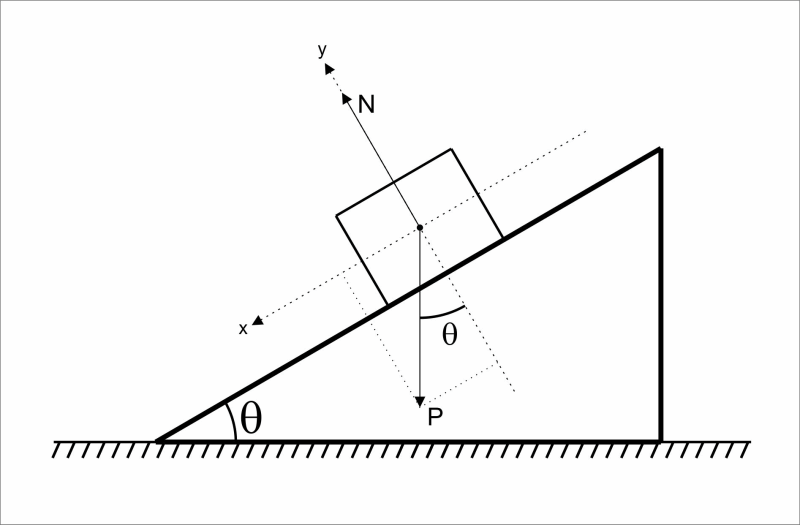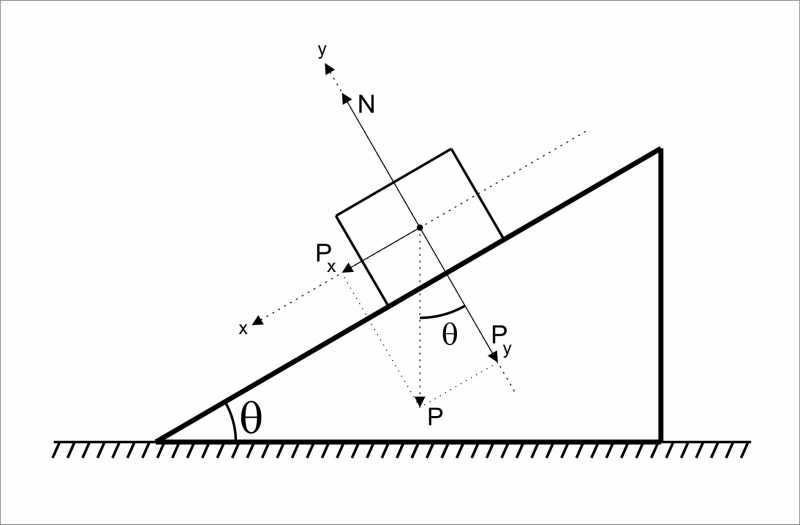
Fazendo a decomposição da força peso obtemos que a força resultante será componente da força peso no eixo x, ou seja, a . Aplicando as razões trigonométricas obtemos:
- Movimento Circular Uniforme
Na figura temos um corpo fixo a um centro por uma corda, apoiado em uma superfície sem atrito. A força peso e a força normal se cancelam, pois estão na mesma direção, em sentidos opostos e possuem o mesmo módulo. Assim a força resultante será a força tensora, representando a força centrípeta.
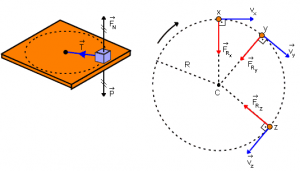
Então aplicando a 2ª Lei de Newton temos:
em que R é o raio da circunferência e v a velocidade tangencial do corpo.
3ª Lei de Newton – Princípio da Ação e Reação
afirma que:

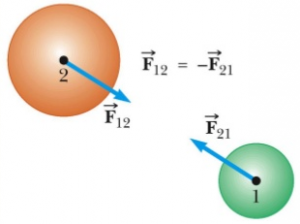
As forças que formam o par de ação e reação estão aplicadas em corpos diferentes e por isso não se cancelam. Assim quando o corpo 1 aplica uma força sobre o corpo 2, esse reage e aplica uma força de mesma intensidade direção e sentido sobre o corpo 1.
Um exemplo comum no nosso dia a dia é o andar sobre a superfície da Terra. Quando aplicamos uma força empurrando a Terra para trás, instantaneamente ela empurra a gente para frente.
Se a força que o homem exerce na Terra é igual e tem a mesma intensidade da força que a Terra exerce no homem, então por que a Terra também não se move?
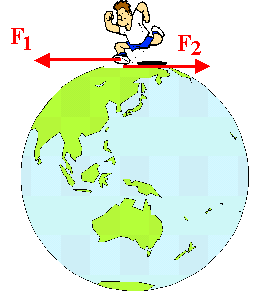 A resposta está relacionada com a Inércia do corpo corpo, isto é quanto maior for a Inércia do corpo menor será sua aceleração.
A resposta está relacionada com a Inércia do corpo corpo, isto é quanto maior for a Inércia do corpo menor será sua aceleração.
Considerando a 2ª Lei de Newton temos:
Considerando a Terra como corpo 1 e o homem como corpo 2, temos que é a força que a Terra exerce sobre o homem e
a força que o homem exerce sobre a Terra. Então se:
O mesmo acontece com o satélite orbitando a Terra. Considerando os módulos de forças iguais, como a massa da Terra é maior que a massa do satélite, a sua aceleração é muito pequena para ser detectada.
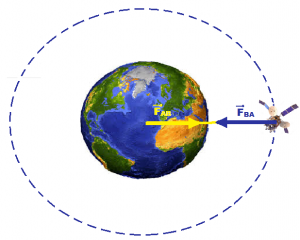
é a força que o satélite exerce sobre a Terra e
é a força que a Terra exerce sobre o satélite.







