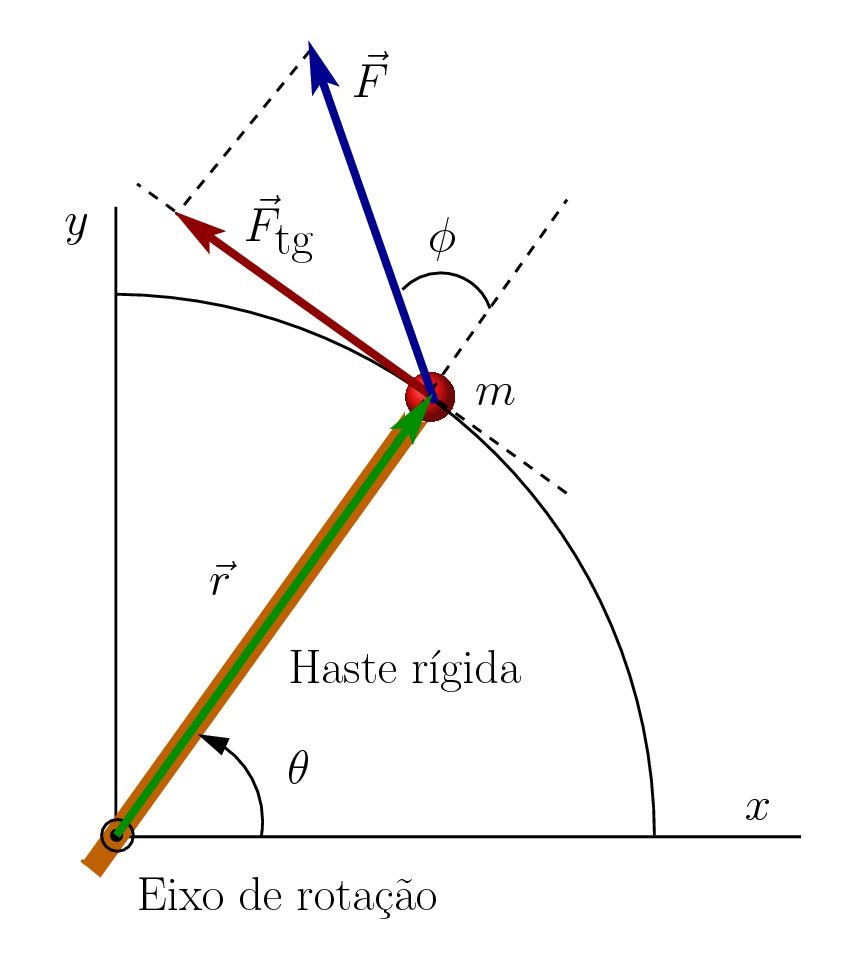
Trabalho para o Movimento de Rotação

Em Trabalho e Energia Cinética, discutimos o conceito de trabalho e a sua relação com a energia cinética de um corpo, quando este sofre uma translação. Agora vamos trazer esse conceito para o movimento de rotação e estabelecer a sua relação com a energia cinética de rotação.

Recordando, trabalho é a transferência de energia de um sistema a um corpo ou vice-versa, através de uma ou mais força. Quantitativamente, é definida como sendo

$W = F \Delta x$

A expressão acima é bastante limitada, na verdade. Ela só é válida se a força for constante e na direção/sentido do deslocamento.

Se tomarmos ainda uma força ao longo do caminho, mas desta vez variável, o trabalho de uma posição $s_i$ até $s_f$ é dado por

$W=\int_{s_i}^{s_f}Fds \quad (1)$

Através da expressão acima, calculamos o trabalho de uma força elástica da mola, da força gravitacional de Newton, da força de Coulomb, etc.

Fazendo a correspondência com o movimento de translação e rotação, temos que o corresponde da força $F$ é o torque $\tau$ e do deslocamento $\Delta s$ o deslocamento angular $\Delta \theta$ . Assim, podemos escrever o trabalho de um corpo girando em torno de um eixo fixo como:

$W=\int_{\theta _i}^{\theta _f}\tau d\theta \quad (2)$

Para quem se interessar, partirmos da Eq. (1) e mostramos que o trabalho pode ser dado pela Eq. (2).

Clique aqui para abrir a demostração.

Teorema Trabalho – Energia Cinética para movimento de rotação

No movimento de translação vimos que o trabalho de uma força resultante sobre um corpo de massa $m$ é igual a sua variação da energia cinética:

$W=\Delta K=K_f-K_i=\frac {1}{2}m v_f^2 - \frac {1}{2}m v_i^2$

Se lembrarmos da correspondência entre a velocidade de translação $v$ e a velocidade de rotação $\omega$ e a massa $m$ com o momento de inércia, esperaríamos que a energia cinética de rotação é

$K_\textrm{rot} = \frac{1}{2} I \omega^2$

De fato, isso é observado, pois $v = \omega r$ e portanto

$K = \frac{1}{2} m v^2 = \frac{1}{2} m r \omega}^2 = \frac{1}{2} I \omega^2,$

onde identificamos $mr^2$ como sendo o momento de inércia do corpo.

Em vista disso, o teorema trabalho-energia cinética para um corpo executando um movimento circular deve ser

$W_\textrm{tot} =\frac {1}{2} I \omega _f^2-\frac {1}{2} I \omega _i^2$

O teorema acima pode ser mostrado, de fato, partindo da Eq. (2) e lembrando-se da segunda lei de Newton para rotações:

$\tau_\textrm{res} = I \alpha$

A matemática é similar a aquela usada para demonstrar o teorema trabalho-energia cinética na página Trabalho e Energia Cinética para forças variáveis.

Clique aqui para abrir a demostração.