A Energia Cinética de Um Corpo Rolando
Quando discutimos um processo de colisão, é comum ilustrarmos o fenômeno através da colisão entre bolas de bilhar. Quando afirmamos que esse tipo de colisão é elástica e portanto usamos a equação da conservação da energia cinética,
![]()
não estamos levando em conta que as bolas estão rolando! No entanto, como as bolas estão rolando, é preciso contabilizar a energia cinética de rotação das bolas.
Embora não seja tão comum, as vezes utilizamos uma bolinha rolando ladeira abaixo para ilustrar a conservação da energia total (mecânica) do sistema. Se uma bola de massa ![]() rola de uma rampa de altura
rola de uma rampa de altura ![]() , qual a sua velocidade na base da rampa?
, qual a sua velocidade na base da rampa?
Sem hesitar, fazemos
![]()
O movimento de uma bola rolando é uma combinação de movimento de translação, que é o movimento do centro de massa da bola, e de rotação, com a bola girando em torno de um eixo que passa pelo centro de massa. Neste caso, o eixo de rotação sofre uma translação. Em suma, trata-se de um movimento combinado.
De acordo com o discutido na seção anterior, a energia cinética de rotação é dada por
![]()
Se o corpo de raio ![]() estiver rolando e possuir velocidade de translação
estiver rolando e possuir velocidade de translação ![]() , como escrever a energia cinética total?
, como escrever a energia cinética total?
Antes de responder a essa pergunta, temos que entender o que é a velocidade ![]() da bola? Se ela não estive deslizando, a velocidade instantânea da bola no ponto de contato com o chão é zero. Se não for, estará deslizando.
da bola? Se ela não estive deslizando, a velocidade instantânea da bola no ponto de contato com o chão é zero. Se não for, estará deslizando.
Seguindo a análise, é razoável esperar que o centro de massa da bola, que descreve um movimento retilíneo, da bola rolando em linha reta, deva possuir velocidade ![]() , também num movimento retilíneo.
, também num movimento retilíneo.
Por outro lado, se a bola só gira, com o seu centro de massa em repouso, as velocidades nas extremidades de baixo e de cima estão na mesma direção, mas em sentidos opostos.
Posto isto, podemos entender o movimento de rolamento como sendo uma combinação de dois movimentos: translação pura e rotação pura. A figura abaixo nos ajuda a compreender a velocidade nos três pontos principais: no centro de massa, no topo e na base:
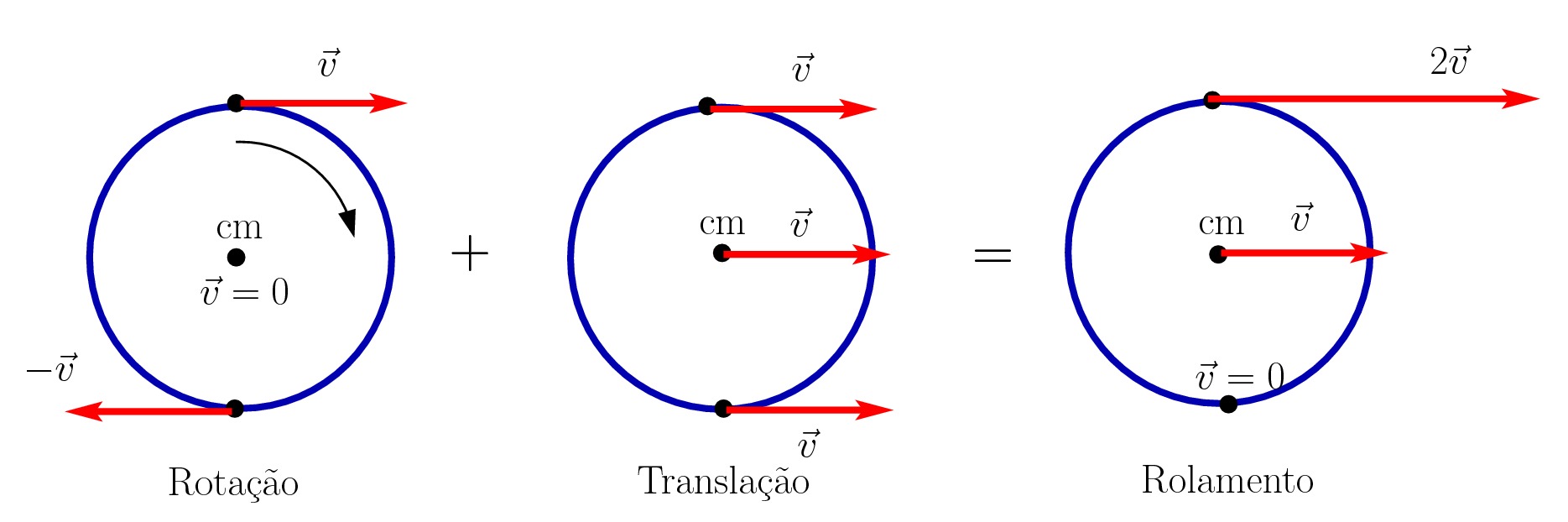
Temos portanto que a energia cinética de rolamento é a soma das energias cinéticas de rotação e translação, ou seja,
![]()
onde ![]() é o momento de inércia do objeto em relação ao eixo que passa pelo seu centro de massa.
é o momento de inércia do objeto em relação ao eixo que passa pelo seu centro de massa.
Como ![]() , temos que
, temos que
![]()
A Competição dos Cilindros Rolando
Vamos supor dois objetos cilíndricos de mesma massa ![]() e raio
e raio ![]() . O primeiro é maciço, enquanto o segundo é uma casca cilíndrica.
. O primeiro é maciço, enquanto o segundo é uma casca cilíndrica.
Se colocarmos os dois cilindros a uma altura ![]() para descer por um plano inclinado, qual deles chegará primeiro à base do plano? Vamos tomar cuidado para que ambos os cilindros rolem pelo plano, sem que ocorra o deslizamento.
para descer por um plano inclinado, qual deles chegará primeiro à base do plano? Vamos tomar cuidado para que ambos os cilindros rolem pelo plano, sem que ocorra o deslizamento.
Pela conservação da energia total do sistema (mecânica), temos que
![]()
Estamos tomando a energia potencial em relação ao centro de massa dos objetos e que ![]() quando os mesmos se encontram na base da rampa.
quando os mesmos se encontram na base da rampa.
Como os momentos de inércia do cilindro sólido e da casca cilíndrica com respeito ao eixo que passa pelo centro de massa são
![]()
podemos escrever ![]() , onde
, onde ![]() para o cilindro maciço e 1 para a casca cilíndrica. Logo, a velocidade na base da rampa é dada por
para o cilindro maciço e 1 para a casca cilíndrica. Logo, a velocidade na base da rampa é dada por
![]()
Como o cilindro maciço possui ![]() menor, adquire velocidade maior. Isso significa que ele deve chagar antes na base da rampa.
menor, adquire velocidade maior. Isso significa que ele deve chagar antes na base da rampa.
O vídeo abaixo testa se a predição teórica de fato é observada.
Vídeo: Inércia de rotação







