Energia Mecânica e a Sua Conservação

Discutimos até aqui duas formas de energia: a energia cinética, que está associada a um corpo em movimento e a energia potencial, que é uma energia “armazenada” por um sistema. Por “sistema”, entendemos como sendo o universo físico constituído por um ou mais corpos móveis sob ação de uma ou mais forças conservativas.

Caso o sistema se encontra isolado, podemos juntar dois resultados encontrados até aqui, a saber,

Pelo teorema trabalho-energia cinética, o trabalho de uma força resultante é igual a variação da energia cinética do corpo:
$W_r = \Delta K = K_f - K_i$
Caso uma força conservativa haja num corpo, a energia potencial do sistema é dada por
$W = -\Delta U = -(U_f - U_i)$

Caso uma força conservativa seja também a força resultante, podemos igualar as duas expressões acima, obtendo

$K_f-K_i=-(U_f-U_i) \quad \Rightarrow \quad K_f+U_f=K_i+U_i$

A fórmula do lado direito mostra que a grandeza $K+U$ calculada no final do processo (subíndice $f$ ) é igual a do início (subíndice $i$ ), ou seja, ela é conservada. Definimos a soma $K+U = E$ como sendo a energia do sistema. Temos que

A energia do sistema, que é a soma das energias cinética e potencial, se conserva em um sistema fechado, onde só atuam forças conservativas.

É muito comum chamarmos a energia do sistema como a energia mecânica do sistema. Esta nomenclatura traz confusão quando $U$ é a energia potencial eletrostática ou outra forma de energia, que não a gravitacional e a elástica.

Vídeo 4: O vídeo mostra um experimento no plano inclinado que tem como objetivo verificar a conservação da energia mecânica.

Conservação de energia – forças não conservativas

Se consideramos sistemas em que somente forças conservativas atuam, vimos que a energia do sistema se conserva num processo, ou seja,

$K_i + U_i = K_f + U_f$

O que ocorre com a energia do sistema quando há forças não-conservativas? Por exemplo, a experiência do cotidiano mostra que se dermos um empurrão num bloco sobre uma superfície horizontal, ele desliza, mas eventualmente entra em repouso, por mais que a superfície seja bem lisa. Neste sistema, conforme já discutido, a força responsável para frear o bloco é a força de atrito, que mostramos que é uma força não-conservativa.

Neste exemplo, observamos que $K_i+U_i \neq K_f + U_f$ . Temos que $U_i=U_f=0$ (não há nenhuma força conservativa relevante ao movimento) , mas como o bloco para, $K_f=0 \neq K_i$ .

Mesmo assim, podemos escrever alguma equação de conservação (ou não) de energia? A resposta é sim, baseada na lei da conservação a energia total, uma lei fundamental da Física que afirma que a soma de todas as formas de energia se conserva num determinado processo. Até o presente momento, não há um único fenômeno sequer que viola esta lei da Física. Devemos concluir portanto que além da energia cinética e da energia potencial, há outros tipos de energia.

Numa situação geral, quando forças conservativas e não-conservativas atuam no sistema, o trabalho resultante é dado por

$W_r = W_\textrm{cons} + W_\textrm{ncons}$

onde $W _\textrm{cons}$ é a soma dos trabalhos realizados por forças conservativas e $W _\textrm{ncons}$ é a soma dos trabalhos realizados por forças não-conservativas. Temos que

O trabalho da força resultante é a variação da energia cinética: $W_r = \Delta K = K_f-K_i$
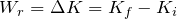
A variação da energia potencial é menos o trabalho das forças conservativas: $W_\textrm{cons} = -\Delta U = -(U_f-U_i)$ .

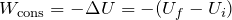Segue portanto que

$K_f -K_i = -(U_f-U_i) + W_\textrm{ncons}$

Logo,

$E_f=E_i+W _\textrm{ncons}$

A energia dissipada, representada por $W _\textrm{ncons}$ , entra com sinal negativo (lembre-se que obtivemos trabalho negativo para a força de atrito), de forma que $E_f < E_i$ .

Mas para onde vai a energia dissipada? No caso do atrito, $W_\textrm{ncons}$ contabiliza a energia retirada do sistema (dissipada), num processo em que a energia do sistema se transforma em calor, que discutimos neste site na página Calor e Primeira Lei da Termodinâmica . De fato, vemos na Termodinâmica que o calor é uma forma de energia.

Há outras formas de energia, além do calor, que são discutidos neste site (clique aqui), como a massa como forma de energia, a energia associada ao campo eletromagnético (não confundir com a energia potencial eletrostática).

Ir para a próxima página: Calor e Primeira Lei da Termodinâmica