Calor

Você passa por situações corriqueiras como por exemplo, um almoço em um dia quente de verão, em que você retira uma jarra de suco da geladeira, deixa sobre a mesa e depois de um tempo percebe que o suco “esquentou”, isto é, sua temperatura aumentou em relação à temperatura de quando o suco foi retirado da geladeira. No mesmo almoço você percebe que a comida “quente” retirada do forno “esfria” depois de um tempo, ou seja, a sua temperatura diminui.

Mas por que isso acontece? Por que os corpos mudam de temperatura?

A resposta para esta pergunta é a transferência (popularmente dita “troca”) de uma forma de energia entre o corpo (suco e comida) e o ambiente devido à diferença de temperatura. A transferência dessa energia é denominada calor (que simbolizamos por $Q$ ), definida como:

Calor é a transferência de energia entre corpos devido à diferença de temperatura entre eles.

A transferência de calor cessa quando ambos os corpos atingem a mesma temperatura, situação esta chamada de equilíbrio térmico. Para efeito de esclarecimento, no nosso exemplo o suco/comida é um corpo e o meio ambiente o outro corpo.

Da mesma forma que o conceito de trabalho, o calor é energia em trânsito. Logo, o termo “calor” utilizado no dia – a – dia difere daquele definido pela Física. Quando dizemos que “hoje está fazendo calor”, na verdade estamos nos referindo à temperatura do ambiente. Os termos “quente” e “frio” são relativos à temperatura, mas tem a questão da sensação térmica, que é baseada na diferença de temperatura e do calor transferido.

De acordo com a segunda lei da termodinâmica

O calor flui de forma espontânea do corpo de maior temperatura para o corpo de menor temperatura.

Afinal, qual a origem do calor? O que ocorre a um corpo quando recebe/cede calor? Para responder a estas perguntas, é importante introduzirmos o conceito de energia interna de um corpo.

Energia Interna

Para entender o conceito de energia interna de um corpo (simbolizada por $U$ ), é importante termos (i) uma noção microscópica da matéria; quais são os constituintes básicos da matéria e as interações entre os mesmos e (ii) o conceito de temperatura.

Qualquer corpo (matéria) é constituído por átomos e moléculas, que estão “grudados” entre si por ligações químicas. Embora existam diferentes tipos de ligações químicas (iônica, covalente, etc.), todas elas são de natureza eletromagnética. Dependendo da temperatura, há diferentes formas desses átomos vibrarem, girarem em torno do seu centro de massa, entre outras formas de se mexerem. A isto, chamamos de agitação térmica. Quanto maior a temperatura, maior a amplitude e as formas de agitação. Os sólidos, por exemplo, podem ser modelados por uma coleção de átomos unidos por molas. Cada átomo pode vibrar em relação à sua posição de equilíbrio.

No caso dos fluidos (líquidos e gases), a estrutura fundamental são moléculas. Além dos movimentos de vibração dos átomos que os constituem, é preciso levar em conta os movimentos das moléculas uma em relação às outras. No caso de gases, ela podem “caminhar” quase que livremente em um recipiente, colidindo eventualmente com outras moléculas e com as paredes do recipiente.

As energias cinéticas de translação (caso dos gases) e a energia de ligação (cinética vibracional mais o potencial) entre átomos e ou moléculas definem a energia interna do corpo. Por outro lado, essa energia interna está relacionada com a sua temperatura. Por conta disto, é comum alguns autores afirmarem que a temperatura é uma grandeza que mede o grau de agitação de um corpo. Não se trata de uma definição precisa de temperatura, mas dá uma noção do que ela é.

É certo que quando um corpo recebe calor, a energia interna aumenta, aumentando o grau de agitação térmica. No entanto, nem sempre isto reflete num aumento de temperatura do corpo. Dependendo das condições, a energia recebida pode quebrar a ligação entre as moléculas do sólido, de forma que elas podem se tornar líquido ou gasoso. Se o corpo em estado líquido ou gasoso ceder calor, pode se tornar um sólido. Nessas situações específicas, a troca de calor levou a uma transição de fase do corpo, com a sua temperatura permanecendo constante.

De uma forma geral, exceto por algumas anomalias, o aumento da temperatura causa aumento na energia interna, o que causa maior amplitude de agitação térmica. Como resultado macroscópico, observamos a dilatação térmica do corpo.

Podemos agora voltar à nossa questão do início da discussão: por que o suco esquentou e a comida esfriou?

A resposta é que como o suco estava a uma temperatura menor que o ambiente (local do almoço), ele absorveu calor do ambiente, fazendo com que a sua temperatura aumente. Neste processo, como o ambiente se comporta como um reservatório térmico (efetivamente a sua temperatura se mantém constante), o suco atinge a temperatura ambiente e o sistema entra em equilíbrio.

Em relação à comida, como inicialmente estava a uma temperatura maior do que a do ambiente, ela cede calor ao mesmo. Após a comida atingir a temperatura ambiente, ambos entraram em equilíbrio térmico.

Levando-se em conta a conservação de energia, somos induzidos a dizer que

$\Delta U = Q, \quad\quad(\textrm{s\'o envolvendo troca de calor})$

ou seja, quando o corpo absorve calor, $Q>0$ , e portanto há aumento na sua energia interna. Por outro lado, ele cede calor, $Q<0$ , e portanto a sua energia interna diminui.

A relação acima é incompleta, pois há um outro mecanismo de transferência de energia que modifica a energia interna do sistema, que já discutimos: trata-se do trabalho $W$ .

Conforme vimos, o trabalho sobre um corpo é a transferência de energia através de uma ou mais forças que agem sobre ele, ao longo da direção do movimento, multiplicadas pelo seu deslocamento.

Um sistema termodinâmico onde o trabalho é bastante relevante é em sistemas formados por gases, visto que a realização do trabalho implica na mudança do seu volume, conforme veremos a seguir.

Trabalho na termodinâmica

Conforme discutido na seção Trabalho e Energia Cinética, em Física o trabalho é definido como sendo a transferência de energia mediante ação de uma ou mais forças que agem num corpo, onde este sofre um certo deslocamento na direção dessa força. Na termodinâmica, o conceito de trabalho também tem esse mesmo significado físico.

Contudo, é comum dividir o trabalho em dois tipos: o trabalho de compressão e expansão, quando há mudança no volume do sistema (caso típico de gás), que denotaremos pelo símbolo $W_c$ e outros tipos de trabalho, como aquele relacionado por exemplo à liberação de energia elétrica numa reação química, resultando na força eletromotriz de uma bateria de carro.

Trabalho de compressão /expansão de um gás

O gás é matéria que se encontra no estado gasoso. Uma amostra de gás tem uma massa bem definida, no entanto o seu volume não é bem definido; ele terá o volume do recipiente que o contém.

Além do volume $V$ , o gás é caracterizado pela pressão $P$ e temperatura $T$ . As variáveis $P, V$ e $T$ , juntamente com o número de mols $n$ caracteriza o estado do gás. Por conta disto, são chamadas de variáveis de estado.

Para o chamado gás ideal, que é um modelo que descreve um gás real bastante rarefeito, vale a seguinte equação de estado:

$PV = n RT$

onde $T$ é a temperatura absoluta (dada em kelvin) e $R$ a chamada constante universal dos gases. No SI de unidades, $R=8,\!3144598(48)\textrm{ J}\cdot\textrm{mol}^{-1}\cdot \textrm{K}^{-1}$ .

Imagine um gás confinado em um recipiente cilíndrico formado por paredes adiabáticas, isto é, paredes que não permitem a troca de calor com o meio externo.

No estado inicial, o gás ocupa um volume $V_{i}$ , possui uma pressão $P_{i}$ e está a uma temperatura $T_{i}$ .

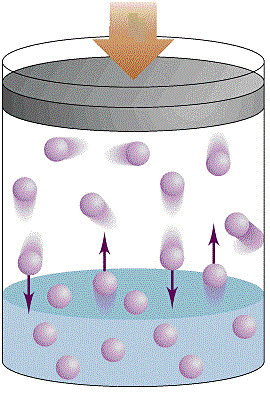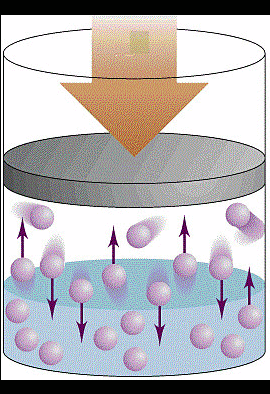Se aplicarmos uma força $\vec{F}$ externa no êmbolo, o volume do gás diminui para $V_f$ e a sua pressão aumenta para $P_f$ .

Mesmo considerando a amostra como um gás ideal, a equação do estado não diz o que ocorre com a temperatura do gás. Contudo, sabendo-se que o êmbolo se deslocou com a força aplicada sobre o gás (transferindo energia para o gás) e que $Q=0$ por conta das paredes adiabáticas, a energia interna do gás aumentou. Neste caso, a temperatura aumenta, pois o gás não sofre transição de fase.

Através dessa análise qualitativa, é convincente que o trabalho realizado pela força externa muda a energia interna do gás.

Vamos agora definir de forma precisa e quantitativa o trabalho no caso em que há compressão ou expansão de um gás, não necessariamente um gás ideal.

Imagine uma certa quantidade de um gás dentro de um pistão, que possui um êmbolo de área $S$ . Evidentemente, se o êmbolo estiver livre, a tendência é o gás empurrá-lo, de forma que haja aumento no volume do gás.

A força que o gás realiza para deslocar o êmbolo é $\vec F$ . Tal força surge por conta da pressão do gás:

$P=\frac{F}{S}\quad \Rightarrow \quad F=PS$

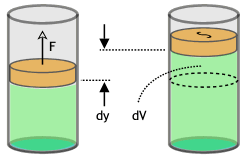
Para obter a expressão do trabalho, vamos considerar o chamado processo quase-estático para levar o sistema de um estado inicial para o estado final. Neste tipo de processo, é executada uma sequência de variações pequenas das variáveis de estado. Com isto, o sistema sempre vai estar em equilíbrio e as variáveis $P, V$ e $T$ estarão bem definidas. Numa mudança brusca, isso não ocorre.

Neste caso específico de processo quase-estático, o volume muda muito pouco quando o êmbolo se deslocado de uma quantidade infinitesimal $dy$ (na figura acima, o tamanho $dy$ está exagerado). Durante esse deslocamento, podemos considerar a força como sendo constante. Logo, o trabalho (infinitesimal) de compressão ou expansão realizado pelo gás é dado por

$dW_c = F \: ds \quad \Rightarrow \quad dW_c = P S \: dy = P \: dV$

Observamos que $S dy$ corresponde à mudança de volume infinitesimal $dV$ do gás.

Para uma mudança finita do volume, de $V_i$ para $V_f$ , o trabalho é dado por

$W_c = \int_{V_i}^{V_f} P \: dV$

Pensando em um gráfico de pressão em função do volume, temos que o trabalho é numericamente igual a área abaixo do gráfico $P(V)$ :

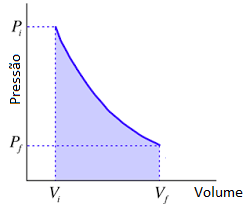
Em princípio, não há como realizar a integração sem conhecer a função $P(V)$ ; o trabalho depende de como a pressão varia em função de volume quando o gás muda de um estado inicial $V_i$ para um estado final $V_f$ , isto é, qual o tipo de processo termodinâmico o gás sofre.

Dentre as várias possibilidades de processos termodinâmicos, podemos citar os processos

isotérmico (temperatura constante);
isobárico (pressão constante);
isocórico (volume constante);
adiabático (não há troca de calor).

Evidentemente, no processo isocórico $dV=0$ e portanto o trabalho realizado pelo gás será nulo.

Um outro processo simples para se calcular o trabalho é o isobárico. Como $P$ é constante, temos que

$W_c = P \int_{V_i}^{V_f} dV = P (V_f-V_i) \quad \Rightarrow \quad W_c = P \Delta V \quad\quad (\textrm{processo isob\'arico})$

No caso específico de um gás ideal, podemos obter as expressões de trabalho para cada um dos processos utilizando-se a equação de estado $PV = nRT$ .

Agora que aprendemos a calcular o trabalho realizado pelo sistema (particularmente para um gás ideal), podemos discutir quantitativamente a relação entre o trabalho e a energia interna. Se o sistema realizou um trabalho $W_c$ positivo, há a expansão do volume. Como há um gasto para fazer isto, a energia interna deve diminuir. Logo,

$\Delta U = -W_c \quad\quad (\textrm{sistema fechado, sem troca de calor})$

O sinal negativo é para dar conta de que a energia interna diminui quando o sistema realiza um trabalho positivo. Caso contrário, a energia aumenta. No caso em que $W_c<0$ , é mais fácil interpretar que uma força externa realizou um trabalho sobre o sistema, ou seja, $W_\textrm{externo} = -W_c >0$ .

O que ocorre se o sistema que acabamos de discutir não estivesse isolado, ou seja, se houvesse calor trocado? Vamos responder a esta questão na próxima seção.

A Primeira Lei da Termodinâmica

Nas seções anteriores, identificamos separadamente duas formas de transferência de energia entre um sistema e sua vizinhança: o calor $Q$ e o trabalho de compressão ou expansão $W_c$ .

Em uma situação geral, processos termodinâmicos podem envolver simultaneamente troca de energia por calor e por trabalho. A primeira lei da termodinâmica leva em conta essas duas formas de energia em trânsito (saem ou entram no sistema) e afirma que a energia total deve ser conservada:

Para qualquer processo em que se acrescenta calor $\textcolor{azul}{Q}$ a um sistema e trabalho $\textcolor{azul}{W}$ é realizado pelo sistema, a energia resultante transferida, $\textcolor{azul}{Q-W}$ , é igual à variação de energia interna $\textcolor{azul}{\Delta U}$ do sistema.

Em forma de equação, temos que

$\Delta U=Q-W$

É importante observar que conforme visto acima, o trabalho depende do tipo de processo termodinâmico. Ou seja, possui valores diferentes para processos termodinâmicos distintos que levam de um estado inicial com $V_i, P_i, T_i, n_i$ para o estado final $V_f, P_f, T_f, n_f$ .

Por outro lado, vamos afirmar aqui sem provas de que a variação da energia interna $\Delta U = U_f - U_i$ só depende dos estados inicial e final – qualquer processo termodinâmico que conecta esses estados produz a mesma variação da energia interna. Para o caso de um gás ideal, é possível mostrar que a energia interna é diretamente proporcional à temperatura do sistema.

Com as observações acima para $\Delta U$ e $W$ e da relação $Q= \Delta U +W$ , decorrente da primeira lei da termodinâmica, fica evidente que $Q$ depende do tipo de processo, assim como $W$ . De fato, experimentalmente verifica-se que o calor trocado depende do processo termodinâmico o qual conecta os estados inicial e final.

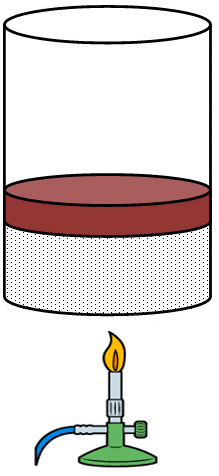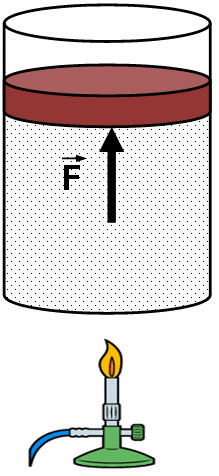
A figura ao lado mostra um sistema formado por um gás contido num pistão móvel, em uma situação em que tanto o calor como o trabalho são diferentes de zero. Se o calor $Q$ for adicionado ao gás e o êmbolo for móvel, é possível manter a temperatura do gás constante. No caso, teremos um processo isotérmico. Nesta situação, o sistema recebe calor e imediatamente realiza trabalho, de forma que a sua energia interna permanece constante.

A primeira lei da termodinâmica e a energia total do sistema

Na seção Energia potencial vimos que a energia transferida pelo trabalho é armazenada na forma de energia potencial. Esta energia é o negativo do trabalho é a variação da energia potencial $-W=\Delta U$ . Voltando para o sistema termodinâmico (gás) temos que a energia transferida pelo trabalho é armazenada na forma de energia interna $U$ .