Energia Potencial
Na seção “Trabalho e Forças Conservativas”, discutimos o que são forças conservativas. Por outro lado, devemos lembrar que o trabalho é a transferência de energia realizada por uma força ou conjunto de forças que agem num corpo.
Quando se tem o trabalho de uma força resultante, mostramos o teorema do trabalho-energia cinética:
![]()
A pergunta natural que se faz é a seguinte: para onde vai a energia quando o trabalho é negativo (corpo perde energia)?. Similarmente, de onde vem a energia quando o trabalho é positivo (corpo ganha energia)?
A animação abaixo mostra a oscilação de um pêndulo simples.
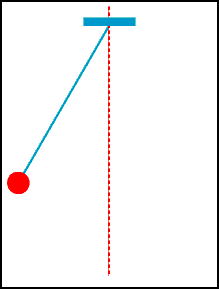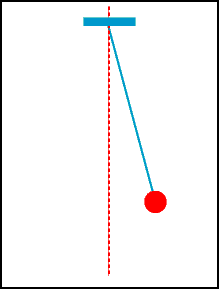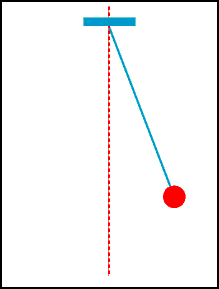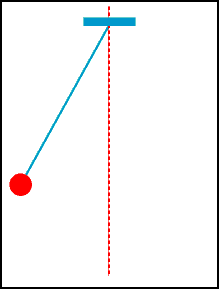
Embora existe a força de tração do fio (caso contrário estaria em queda livre!), podemos concentrar na força gravitacional (força peso) agindo sobre a massa pendurada pelo fio. Claramente a energia cinética da massa varia com a posição do pêndulo. Por outro lado, já vimos que o trabalho da força gravitacional transfere energia para a massa na descida e retira energia na subida. Afinal, de onde vem e para onde vai essa energia transferida?
Como resposta, a energia transferida pelo trabalho é armazenada no sistema (no caso do pêndulo, o sistema é formado pelo pêndulo em si e a Terra, responsável por gerar a força gravitacional). Esta energia é chamada de energia potencial. A sua variação – energia potencial final menos a inicial, é definida como sendo
![]()
Como ![]() só depende das posições inicial e final, é importante enfatizar que a energia potencial só é definida em termos do trabalho de forças conservativas.
só depende das posições inicial e final, é importante enfatizar que a energia potencial só é definida em termos do trabalho de forças conservativas.
A força de atrito, por exemplo, é uma força não-conservativa, como vimos. Logo, não faz sentido algum definir uma “energia potencial de atrito”.
Temos assim que, por definição,
Para recordar, no caso unidimensional com força variável, temos:
![]()
onde ![]() é a posição inicial do corpo, quando a energia potencial do sistema é
é a posição inicial do corpo, quando a energia potencial do sistema é ![]() e
e ![]() a posição final, quando a energia potencial é
a posição final, quando a energia potencial é ![]() , ou seja,
, ou seja,
![]()
Em princípio, existe uma função matemática ![]() , mas somente a sua variação tem significado físico. Logo, podemos definir a energia potencial a menos de um valor numérico constante. Na prática, isso quer dizer que podemos escolher
, mas somente a sua variação tem significado físico. Logo, podemos definir a energia potencial a menos de um valor numérico constante. Na prática, isso quer dizer que podemos escolher ![]() para algum valor de referência de
para algum valor de referência de ![]() , de acordo com a nossa conveniência.
, de acordo com a nossa conveniência.
A seguir, vamos calcular a energia potencial associada a forças conservativas mais recorrentes na Física. Como para algumas forças conservativas nós já calculamos o trabalho, não vamos repetir novamente os cálculos.
Energia potencial gravitacional – próxima à superfície da Terra
Na seção Trabalho e Forças Conservativas, mostramos que para a situação abaixo, o trabalho da força gravitacional de ![]() até
até ![]() é
é
![]()
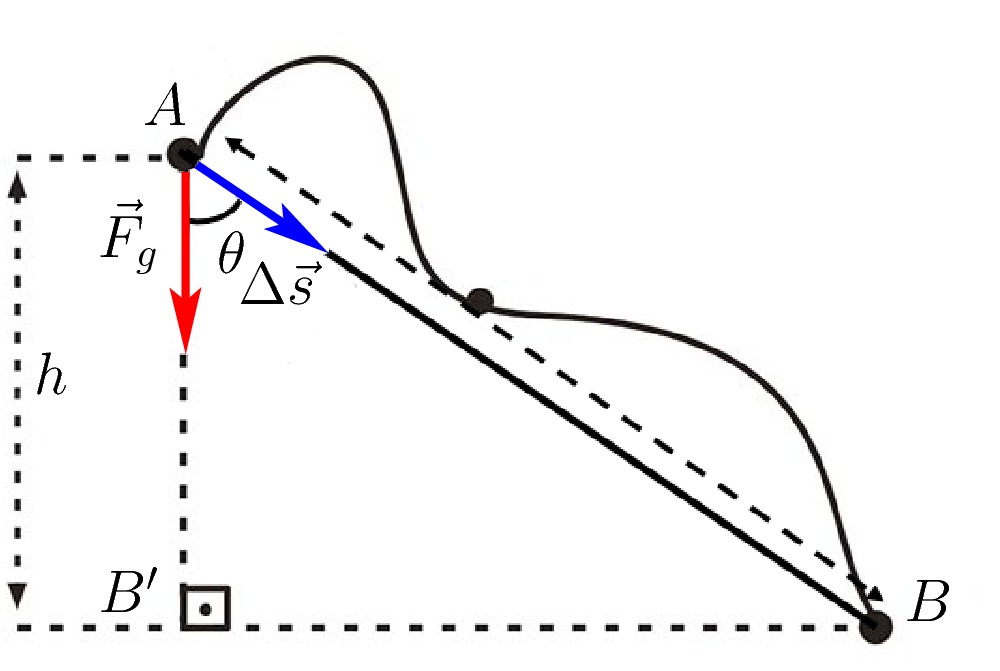
Fazendo a posição ![]() como sendo a inicial e
como sendo a inicial e ![]() a final e tomando um eixo vertical
a final e tomando um eixo vertical ![]() positivo para cima, a energia potencial gravitacional é dada por
positivo para cima, a energia potencial gravitacional é dada por
![]()
Vamos tomar como a origem da coordenada (![]() ) a base do triângulo, onde se encontram os pontos
) a base do triângulo, onde se encontram os pontos ![]() e
e ![]() . Se assumirmos que nesse ponto a energia potencial é zero (
. Se assumirmos que nesse ponto a energia potencial é zero (![]() ), temos que para uma altura
), temos que para uma altura ![]() , a energia potencial gravitacional será
, a energia potencial gravitacional será
![]()
Quanto maior a altura (![]() maior), maior será energia potencial do sistema Terra-corpo. É claro que
maior), maior será energia potencial do sistema Terra-corpo. É claro que ![]() tem limitação, pois estamos assumindo aqui que
tem limitação, pois estamos assumindo aqui que ![]() , onde
, onde ![]() é constante. Para alturas não desprezíveis em relação ao raio da Terra, temos que usar a energia potencial gravitacional calculada a partir da força gravitacional de Newton, que é o exemplo a seguir.
é constante. Para alturas não desprezíveis em relação ao raio da Terra, temos que usar a energia potencial gravitacional calculada a partir da força gravitacional de Newton, que é o exemplo a seguir.
Energia potencial gravitacional – caso geral
Conforme visto na seção Trabalho e Forças Conservativas, o trabalho da força gravitacional quando um corpo 2, de massa ![]() , se desloca de distância
, se desloca de distância ![]() para
para ![]() em relação a um corpo 1, de massa
em relação a um corpo 1, de massa ![]() , é
, é
![]()
Portanto,
![]()
Neste caso, é conveniente tomar ![]() para
para ![]() , ou seja, os dois corpos estão separados por uma distância tendendo a infinito. Fazendo
, ou seja, os dois corpos estão separados por uma distância tendendo a infinito. Fazendo ![]() para
para ![]() , obtemos
, obtemos
![]()
Energia potencial gravitacional – discussões
Antes de ir para mais um exemplo de energia potencial, convém confrontarmos os diferentes resultados da energia potencial gravitacional:
![]()
Vamos mostrar mais adiante que a equação à esquerda é um caso particular da equação à direita. Isto não é surpresa alguma, se entendermos a relação entre as forças relacionadas às duas energias potenciais:
![]()
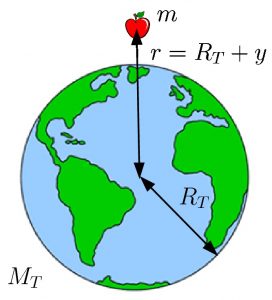
Vamos considerar a equação à direita acima para um caso particular em que o corpo 1 é a Terra, de massa ![]() , e o corpo 2 a maçã, de massa
, e o corpo 2 a maçã, de massa ![]() . Se a maçã estiver a uma altura
. Se a maçã estiver a uma altura ![]() em relação à superfície da Terra, temos que
em relação à superfície da Terra, temos que
![]()
onde ![]() é o raio da Terra.
é o raio da Terra.
Em módulo, a força gravitacional que atrai a maçã para a Terra é dada por
![]()
Na segunda igualdade, apenas colocamos em evidência ![]() no denominador. Observamos que podemos fazer uma expansão binomial com expoente negativo para
no denominador. Observamos que podemos fazer uma expansão binomial com expoente negativo para ![]() . Para um inteiro positivo
. Para um inteiro positivo ![]() ,
,
![]()
Na situação que estamos tratando, ![]() deve ser muito menor do que
deve ser muito menor do que ![]() (ou
(ou ![]() , na linguagem matemática). Por exemplo, se
, na linguagem matemática). Por exemplo, se ![]() for da ordem de 1 km de altura, como a Terra possui um raio médio aproximado de 6370 km, temos que
for da ordem de 1 km de altura, como a Terra possui um raio médio aproximado de 6370 km, temos que ![]() , que evidentemente é muito menor do que 1. Logo, só vamos manter o primeiro termo na expansão binomial, que é 1. Portanto,
, que evidentemente é muito menor do que 1. Logo, só vamos manter o primeiro termo na expansão binomial, que é 1. Portanto,
![]()
onde ![]() m/s
m/s![]() é o módulo do campo gravitacional produzido pela Terra, próximo a sua superfície (
é o módulo do campo gravitacional produzido pela Terra, próximo a sua superfície (![]() ).
).
Vamos agora mostrar que ![]() é equivalente a
é equivalente a ![]() próximo à superfície da Terra. Temos que na posição onde se encontra a maçã na figura acima, o potencial é
próximo à superfície da Terra. Temos que na posição onde se encontra a maçã na figura acima, o potencial é
![]()
Vamos novamente usar a fórmula da expansão binomial, agora com expoente ![]() e mantermos os dois primeiros termos:
e mantermos os dois primeiros termos:
![]()
O primeiro termo é apenas uma constante. Lembrando que podemos escolher o zero da energia potencial gravitacional, observamos que só o segundo termo é importante (por isto, mantivemos dois termos na expansão). Mas no segundo termo, já havíamos identificado ![]() como sendo
como sendo ![]() , logo a demonstração se completa.
, logo a demonstração se completa.
Energia Potencial Eletrostática
Para falarmos sobre a energia potencial eletrostática, temos que apresentar primeiro a força eletrostática, que é dada pela lei de Coulomb, que trata da força mútua entre dois objetos carregados eletricamente.
De acordo com a lei de Coulomb,
Assim como ocorre na lei da gravitação universal, a lei de Coulomb descreve uma força conservativa e fundamental a Natureza que é inversamente proporcional ao quadrado da distância. A diferença principal é que enquanto só há massas de um “tipo”, cargas elétricas possuem dois tipos: as positivas e as negativas. Com isto, embora a direção da força eletrostática não dependa dos tipos de carga, o sentido depende:
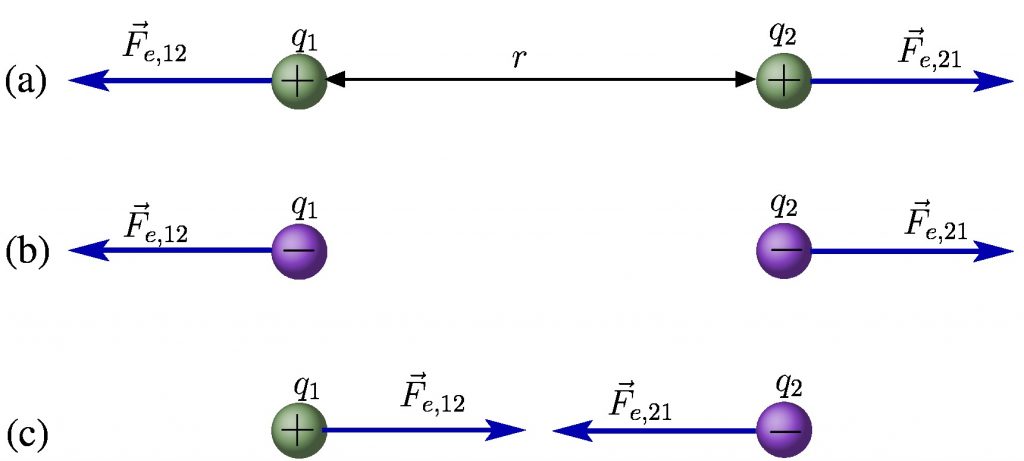
Cargas do mesmo sinal se repelem e de sinais contrários se atraem. O módulo da força é dado por
![]()
onde![]() é a distância entre as cargas puntiformes
é a distância entre as cargas puntiformes ![]() e
e ![]() . A constante, para as duas cargas no vácuo (válido também com boa aproximação para o ar) é
. A constante, para as duas cargas no vácuo (válido também com boa aproximação para o ar) é
![]()
quando as cargas ![]() e
e ![]() devem ser dadas em unidades de coulomb (C).
devem ser dadas em unidades de coulomb (C).
Similarmente às forças gravitacionais entre dois corpos, as forças eletrostáticas também formam um par ação-reação, ou seja,
![]()

Como a fórmula matemática da força eletrostática é similar à da força de gravitação universal, não há necessidade de repetirmos todo o cálculo novamente para encontrar a energia potencial eletrostática. Vamos utilizar o resultado encontrado para a força gravitacional e fazer as adequações. Em especial, atente que no cálculo da trabalho da força eletrostática não há um sinal “![]() ” colocado explicitamente no caso da força gravitacional, visto que cargas iguais se repelem, enquanto massas sempre se atraem. Temos portanto que
” colocado explicitamente no caso da força gravitacional, visto que cargas iguais se repelem, enquanto massas sempre se atraem. Temos portanto que
![]()
Novamente, podemos escolher um valor de referência em que a energia potencial é zero. É conveniente fazermos ![]() para
para ![]() . Tirando o subíndice “
. Tirando o subíndice “![]() ” de
” de ![]() e
e ![]() , temos
, temos
![]()
Energia potencial elástica
Assim como o caso da força gravitacional universal, nós já calculamos o trabalho da força elástica da mola, que se trata também de uma força conservativa. Logo, podemos associar a ela e ao corpo a energia potencial elástica.
![]()
O ponto de referência usual é tomar o zero da energia potencial quando a mola está relaxada, ou seja, para ![]() ,
, ![]() . Novamente, suprimindo o subíndice “
. Novamente, suprimindo o subíndice “![]() “, obtemos a energia potencial elástica da mola:
“, obtemos a energia potencial elástica da mola:
![]()