O Modelo Atômico de Bohr

Antes de descrever o modelo atômico de Niels Bohr vamos fazer uma breve apresentação dos fatores que levaram Bohr a estabelecer seu modelo.

Na teoria clássica do eletromagnetismo, os cientistas buscavam explicar o fenômeno da radiação do corpo negro, porém os dados obtidos se mostravam incompatíveis com a teoria ondulatória de Maxwell. Esses resultados foram chamados de “catástrofe do ultravioleta”, pois foi possível verificar que para comprimentos de ondas menores a intensidade da radiação emitida tendia para o infinito.

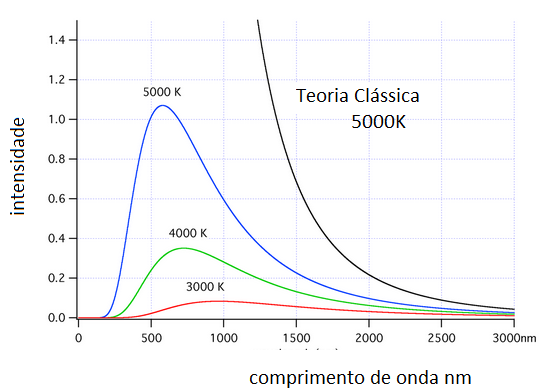
A simulação a seguir permite verificar a emissão de radiação em função do comprimento de onda.

Anos mais tarde o físico Max Planck descobriu uma solução para a incoerência entre a física clássica e o fenômeno observado. Ele concluiu que a radiação eletromagnética é absorvida ou emitida por pacotes discretos de energia (fótons).

A energia estabelecida é determinada pela equação

$E=hf$

onde $f$ é a frequência da radiação e $h$ é a constante de Planck com valor de $6,626\times 10^{-34}Js$ .

Se analisarmos a unidade $Js$ podemos identificar a dimensão da constante de Planck.

$Js=Nms=kg\frac {m}{s^2}}ms=kg\frac {m}{s}m$

A análise mostra que temos a unidade de momento linear $kg\frac {m}{s}$ multiplicada por uma grandeza de comprimento $m$ . Já vimos na seção Momento Angular que essa unidade representa o momento angular.

De acordo com a teoria eletromagnética de Maxwell, os elétrons ao girarem em torno do núcleo do átomo (movimento circular uniforme), deveriam irradiar ondas eletromagnéticas, perder energia e a estabilidade do núcleo.

A figura a seguir mostra a emissão de energia quando os elétrons transitam entre as camadas.

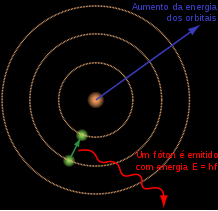
Para Niels Bohr o modelo atômico era representado por um núcleo central o qual era orbitado por elétrons. A partir da quantização da energia ele estabeleceu que o átomos se mantinham estáveis por causa do momento angular do elétron.

Bohr acreditava que o momento angular tinha alguma relação com a constante de Planck, pois a radiação já havia sido quantizada, então ele acreditava que existia uma simetria entre o comportamento da radiação e do átomo, já que a radiação tem comportamento de onda e partícula.

Espectros de Linha

Para vermos a estrutura ou funcionamento interno de um dispositivo como relógio mecânico ou um motor elétrico, expomos o objeto à luz. Com um bom microscópio podemos resolver detalhes da estrutura que se aproxima do limite de resolução, que é determinado pela faixa de comprimento da luz visível, cerca de 400 a 750nm. No entanto não podemos ver diretamente a estrutura de um átomo porque seu tamanho, cerca de 0,1nm, é inferior ao comprimento de onda da luz visível. A estrutura de um átomo ou molécula pode ser estudada por meio da interação da luz com a matéria, isto é, átomos absorvem e emitem luz de acordo com sua estrutura.

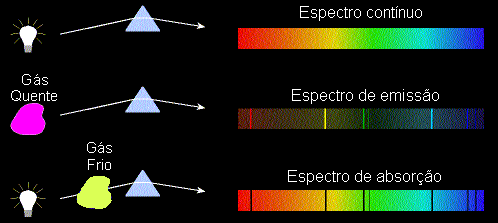
Se a luz de uma cavidade é examinada com um espectômetro, a distribuição de intensidade contém todos comprimentos de onda no intervalo dispersados pelo espectômetro e o conjunto de linhas é chamado de espectro contínuo. A figura a seguir representa o espectro contínuo da luz.

Em contraste, a luz emitida por um anúncio de neon contém luz intensa em um conjunto discreto de comprimentos de onda. Cada comprimento de onda dessa fonte forma uma imagem em uma chapa fotográfica na entrada do espectômetro, de forma que a chapa contém uma sequência de linhas chamada de espectro de linhas.

A figura a seguir mostra o espectro do átomo de hidrogênio.

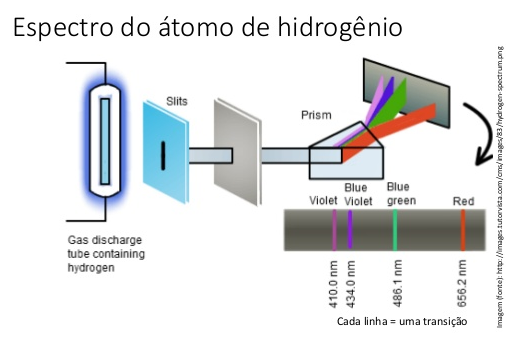
O espectro de luz emitido por uma fonte chama-se espectro de emissão. Neste espectro apresenta-se algumas faixas visíveis do espectro de emissão. Outro tipo de espectro de linhas existentes é o espectro de absorção, que mostra variações para um conjunto discreto de comprimentos de onda. O espectro de absorção é obtido fazendo a luz de espectro continuo passar pela substância substância que irá absorver alguns comprimentos de ondas.

A figura a seguir mostra os espectros de emissão e absorção.

A simulação a seguir permite verificar as linhas espectrais de alguns gases.

O átomo mais leve e mais simples é o átomo de hidrogênio. A figura a seguir mostra seu espectro de emissão.

As linhas $\alpha$ , $\gamma$ , $\lambda$ e $\delta$ estão na parte visível do espectro. As demais linhas estão na região do ultravioleta. O conjunto dessas linhas é chamado de série de Balmer.

John Balmer descobriu uma fórmula matemática para os comprimentos de ondas de linhas visíveis no espectro do hidrogênio. Sua fórmula não tem base teórica é apenas uma relação empírica que descreve corretamente a regularidade no espectro. Além de descrever as quatro linhas visíveis a fórmula também permite calcular o comprimento de onda da parte da série do ultravioleta. Sua fórmula é expressa por:

$\frac{1}{\lambda }=R_{H}\left ( \frac{1}{2^{2}}-\frac{1}{n^{2}} \right )\left ( n=3,4,5... \right )$

onde $R_{H}=1,097.10^{7}m^{-1}$ é a constante de constante de Rydberg para o hidrogênio. Usando $n=3$ na fórmula de Balmer, o comprimento de onda calculado é $lambda =656,3nm$ , sendo o maior comprimento de onda que corresponde a primeira linha $\alpha$ .

Átomo de Hidrogênio

Usando a fórmula de Balmer, Bohr analisou o espectro do hidrogênio verificou que os resultados concordavam com seu modelo. Seu modelo atômico foi apresentado por meio de postulados que seguem:

1º postulado: Um elétron em um átomo, se move em órbita circular estável em torno do núcleo sob interferência da atração coulombiana entre o elétron e o núcleo. Esse movimento está de acordo com as leis da mecânica clássica.

2º postulado: No lugar de um número infinito de órbitas possíveis, como previsto pela mecânica clássica, o elétron só pode se mover em órbitas determinadas, que podem ser associadas a números inteiros.

A órbita possui um momento angular orbital $L$ que é um múltiplo de $n\frac {h}{2\pi}$ . Essas órbitas estáveis são as órbitas as quais o elétron não irradia energia.

Então podemos escrever o momento angular de acordo com a mecânica clássica da seguinte maneira

$L=n\frac {h}{2\pi }=mvr$

A equação mostra a quantização do momento angular.

3º postulado: A frequência da luz emitida está relacionada com a variação de energia entre os níveis de energia que o átomo pode ocupar. A frequência $f$ é dada pela equação de Planck – Einstein como mostra a figura a seguir

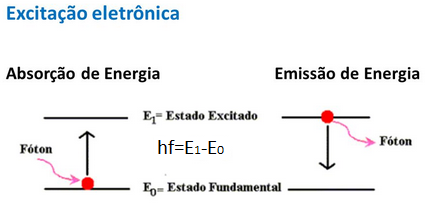
Fazendo uma modelagem matemática podemos estabelecer relações entre os níveis de energia, raio e momento angular.

Primeiramente se o elétron descreve um movimento circular e uniforme temos que a força elétrica é a força resultante, ou seja a força centrípeta. Equacionando temos:

$-F_{cp}=F_{el}\rightarrow \frac{mv^{2}}{r}=\frac {Kq^{2}}{r^{2}}\rightarrow mv^{2}=\frac{Kq^{2}}{r}$

A energia potencial elétrica é $U=-\frac {Kq^{2}}{r}$ e $mv^{2}$ é o dobro da energia cinética, então

$U=-2K$

A energia total é soma entre a energia potencial e cinética então podemos escrever

$E=U+K=U-\frac {U}{2}\rightarrow E=\frac {U}{2}$

Para fazer previsões quantitativas, antecipou outro conceito útil, que corresponde a um modelo quântico em que os estados de energia (estados quânticos) eram descritos por um conjunto finito de órbitas circulares com raios determinados em função do nível de energia.

O raio pode ser definido a partir da força resultante já estabelecida

$-F_{cp}=-F_{el}\rightarrow \frac {mv^{2}}{r}=\frac{Kq^{2}}{r^{2}}\rightarrow r=\frac {q^{2}K}{mv^{2}}$

A equação mostra que o raio é inversamente proporcional ao quadrado da velocidade. Isso mostra que quanto mais próximo o elétron está do núcleo maior é a velocidade e a instabilidade do átomo aumenta.

Considerando o momento angular quantizado $L=n\frac {h}{2\pi }=mvr$ temos que a velocidade pode ser $v=\frac {nh}{2\pi r}$ . Substituindo na equação do raio obtemos

$r=\frac{mn^{2}h^{2}}{4\pi ^{2}Kq^{2}}$

A equação nos mostra que o raio depende de um $n$ que representa o nível de energia. A constante $K$ é a constante elétrica que pode ser escrita como $K=\frac {1}{4\pi \varepsilon _{0}}$ , onde $\varepsilon _{0}=8,854\times 10^{-12}\frac {F}{m}$ e representa a constante de permissividade elétrica.

Substituindo o raio na equação da energia temos

$E=\frac {U}{2}=-\frac {Kq^{2}}{r}=-\frac {q^{4}m}{8\varepsilon _{0}^{2}n^{2}h^{2}}$

As energias são negativas porque a configuração do potencial zero foi definida no infinito em que o elétron está a uma distância muito grande do núcleo e está em repouso.

Quando Bohr estabeleceu seu modelo atômico tudo que ele tinha era a quantização da energia de Planck e o conceito de fóton de Einstein. Algumas de suas afirmações foram derrubadas e em particular o conceito de elétron orbitando o núcleo em órbitas definidas. A ideia de órbita viola a incerteza de Heisenberg, porque ela junta a imagem da partícula com uma quantidade de movimento ocupando uma posição conhecida, quando essas duas variáveis não podem ser determinadas simultaneamente.

Infelizmente o modelo do átomo de Bohr ainda é apresentado como modelo atômico final nas escolas.

No entanto algumas afirmações de Bohr prevaleceram, as equações de energia para o átomo de hidrogênio são as mesmas previstas para o modelo atômico mais avançado, átomo de Schödinger. Também estão corretos a existência dos estados quânticos de energia finita e a validade da condição de frequência de Bohr como parte da fundação da física quântica.

As ideias de Bohr foram de extrema importância para o estímulo do desenvolvimento da física moderna.

A simulação a seguir apresenta os modelos atômicos

Espectros de linhas provenientes do Modelo Atômico de Bohr

De acordo com Bohr, um átomo não irradia quando em estado estacionário. A radiação só é emitida, em forma de fóton, quando um átomo sofre uma transição de um estado estacionário para outro de menor energia. Para ver como essa ideia resulta no espectro do hidrogênio, considere um átomo inicialmente em um estado com número quântico $n$ . A energia de um tal estado é dada inserindo – se $n_{i}$ em lugar de $n$ na equação de energia $E=\frac {U}{2}=-\frac {Kq^{2}}{r}=-\frac {q^{4}m}{8\varepsilon _{0}^{2}n^{2}h^{2}}$ .

Suponha que um átomo sofra uma transição para um estado de energia mais baixa que $n_{i}$ com número quântico $n_{f}$ , de modo que $n_{i}>n_{f}$ . Se um fóton de energia $h$ é emitido n a transição, então, pela conservação de energia

$E_{i}=E_{f}+h\nu$

Como $\nu =\frac {c}{\lambda}$ a equação acima pode ser resolvida em relação a $\frac {1}{\lambda }$ e comparada com a fórmula que contém a constante de Rydberg.

Se as energias são expressas em termos de $n_{i}$ e $n_{f}$ , então a equação pode ser escrita:

$\frac{1}{\lambda }=\frac{mq^{4}}{8\epsilon _{0}^{2}h^{3}c}\left ( \frac{1}{n_{f}^{2}}-\frac{1}{n_{i}^{2}} \right )$

Cada linha do espectro do hidrogênio pode ser associada a uma transição entre dois estados estacionários. Essas transições estão adequadamente mostradas no diagrama de níveis de energia. As linhas horizontais que representam os níveis de energia forma estendidas de forma que se possa mostrar um número de transições.

As transições são dispostas de acordo com as séries vistas no diagrama de níveis de energia a seguir.

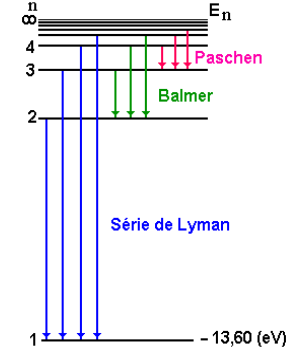
Note que cada linha da série de Lyman é devida a uma transição para o estado fundamental de um estado de energia mais alta. Analogamente, cada linha na série de Balmer corresponde a uma transição para um estado com com $n=2$ de um estado de energia alta. Pelo diagrama pode -se ver como ocorre o limite de uma série em razão da concentração de níveis de próximos a $E=0$ . Se o átomo está no estado fundamental $(n=1)$ , não há nenhum estado de energia mais baixo para o qual possa ocorrer uma transição para baixo. Assim o átomo no estado fundamental é estável.

A Grandeza Física “spin”

Todas as partículas subatômicas, compostas ou elementares, possuem várias propriedades que as caracterizam como tais. Algumas dessas propriedades são também usadas na física clássica, como a massa da partícula (massa de repouso, para ser mais claro) e a carga elétrica.

No entanto, essas partículas subatômicas possuem outras propriedades intrínsecas, cujas origens simplesmente não entendemos. Para caracterizá-las, denominamos de números quânticos, visto que essas propriedades são manifestações explicadas pela mecânica quântica.

Números quânticos

Diferentemente do modelo atômico de Bohr no modelo atômico atual, não só a energia é quantizada mas sim o momento angular, momento magnético e momento spin. No modelo atual cada elétron é caracterizado por um conjunto quatro números quânticos distintos. Vamos começar a explicar o que cada um deles representa.

O primeiro, número quântico principal, aparece no modelo atômico de Bohr representa o nível de energia $n$ , que assume valores inteiros. O segundo, número quântico de momento angular orbital, estabelece os subníveis de energia dentro de um mesmo nível. É representado pela letra $l$ e pode assumir valores que vai de $0$ até $n-1$ , em que $n$ é o número quântico principal.

O terceiro número quântico, número quântico magnético, representado pela letra $m$ indica o orbital individual em que um elétron se encontra dentro de um subnível de energia. Os valores que pode assumir varia entre $-l$ e $l$ , podendo assumir valor igual a zero.

O quarto número quântico é o número quântico magnético spin. Uma dessas propriedades quânticas de partículas, elementares ou compostas, é o chamada de spin. Livros de química do ensino médio associam o spin à rotação do elétron em torno do seu próprio eixo, da mesma forma que a Terra gira em torno do seu próprio eixo em 24 h.

O que há de errado com essa visão? Em primeiro lugar, vamos imaginar o elétron girando em torno do seu próprio eixo.

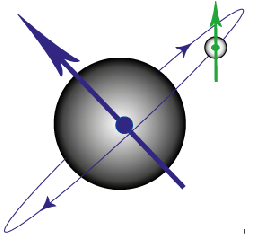
A figura mostra que o elétron gira em torno do núcleo, porém também gira em torno do seu próprio eixo e o spin tem sentido de rotação oposto.

O movimento de rotação foi explicado pelos físicos alemães Otto Stern e Wather Gerlach em um experimento, o qual partiram da hipótese de que os elétrons se comportavam como minúsculos imãs. Seu experimento consistiu em disparar um feixe de átomos de prata entre os polos permanentes de um imã.

O resultado mostrou que os átomos foram distribuídos uniformemente entre o polo sul e norte. Este resultado mostra que os elétrons podem podem apresentar duas direções possíveis: uma favor do campo magnético e outra contra.

O vídeo a seguir apresenta o experimento de Stern – Gerlach.

Essa propriedade do elétron é atribuída à rotação, em que qualquer elétron apresenta spin para cima ou para baixo. Como consequência temos que em um orbital existe no máximo dois elétrons um com spin para cima e outro com spin para baixo. Isso é conhecido como princípio da exclusão de Pauling.

A física de partículas diz que enquanto o elétron é uma partícula fundamental, o próton é constituído por estruturas menores, denominados quarks. Fundamentais ou compostas, as partículas possuem, além da massa e carga elétrica, possuem spin que é uma propriedade intrínseca que representa a quantidade de movimento angular spin.