Vamos agora calcular o momento linear de uma manchete em um jogo de vôlei !

Em uma partida de vôlei, o jogador faz um saque com a bola que é recebida pelo jogador adversário com uma velocidade de . Quando é rebatida pelos braços, a bola passa a ter uma velocidade de . O tempo de em que a bola esteve em contato com a raquete foi de segundo.

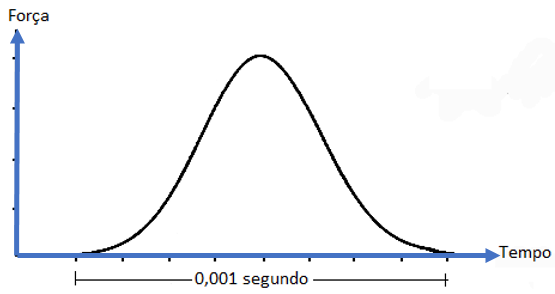
O gráfico representa mostra a força em função do tempo durante o tempo de contato com os braços do jogador.

O gráfico nos mostra que a intensidade da força não é constante, então devemos usar o valor médio.

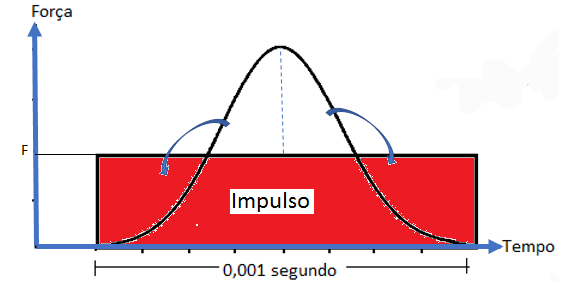
Usando o valor médio temos que a área do retângulo é igual ao impulso, ou seja, a variação da quantidade de movimento.

Vamos primeiro calcular o momento linear antes de ser rebatida. Devemos considerar que a massa da bola é equivalente a e que a velocidade da bola é que corresponde à no sistema internacional de unidades, a velocidade é negaiva tendo em vista a direção do retorno. Então:

   

Agora vamos calcular o momento do retorno. A massa da bola é constante, a velocidade que ao convertermos para o sistema internal de unidades corresponde , com sua orientação positiva.

   

Com os valores dos momentos lineares inicial e final podemos calcular a variação do momento linear correspondente:

   

Como a força agiu durante podemos agora calcular a força aplicada pelo braço usando o teorema do impulso.

   

de força equivale a força aplicada em um de peso que equivale a se considerarmos a aceleração da gravidade . Assim podemos pensar na massa que o jogador poderia levantar ao aplicar a força.

   

O resultado mostra um valor alto de massa para uma pessoa levantar. Não podemos esquecer que a força da gravidade é constante e que isso é apenas momentâneo.

Explorando o impulso no mundo real

Podemos pensar em ais situações o impulso pode estar presente em situações do nosso mundo real. Um exemplo que pode ser citado, o qual podemos verificar a existência do impulso é no esporte de salto. No início da queda a velocidade do atleta é zero, possuindo assim momento linear igual a zero e durante a queda sua velocidade aumenta, atingindo a superfície com velocidade diferente de zero, o que acarreta em um momento linear diferente de zero. Ao atingir a superfície o atleta irá sentir uma força aplicada pela mesma. Para reduzir o impacto da força utiliza-se colchões para amortecer a queda, pois os colchões irá promover um tempo de maior interação entre o corpo do atleta e a superfície diminuindo assim a força aplicada.

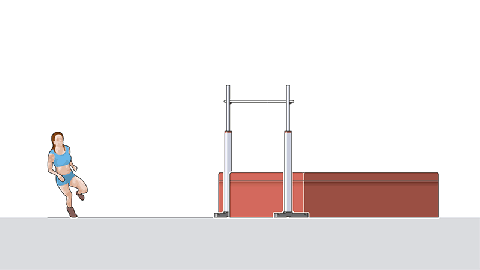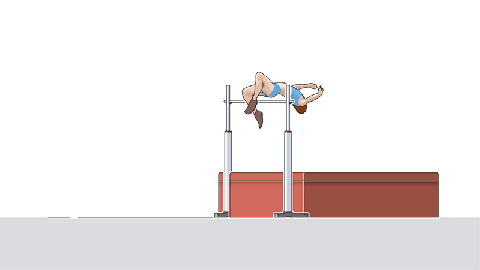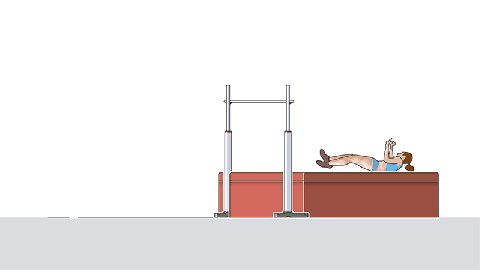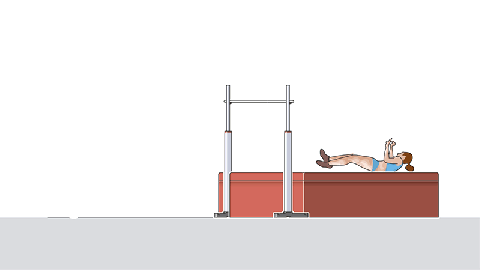
Pela equação do impulso podemos verificar que quanto maior o tempo, menor será a força aplicada.

   

Outro exemplo que também pode ser citado são os airbags presentes no carro. Eles tem a finalidade de amortecer o corpo durante uma batida, ao manter o corpo do motorista em contanto durante mais tempo com o mesmo a força do impacto será reduzida.