A massa é uma grandeza conservada?

Ao longo do tempo, no desenvolvimento da Física e da Química, energia e massa sempre foram consideradas grandezas de naturezas bem diferentes.

É claro que pode existir uma relação direta entre elas. Por exemplo, a energia cinética de um corpo com velocidade $\vec{v}$ é

$K = \frac{1}{2} m v^2$

onde $m$ é a massa do corpo. Quanto maior a massa, maior a sua energia cinética.

No entanto, no que se refere às leis de conservação, energia e massa sempre foram consideradas separadamente até os primeiros anos do século XX.

No período do desenvolvimento da atomística, químicos como Antoine Lavoisier concluíram que a massa era uma quantidade conservada, ou seja, ela é mesma antes e depois de uma reação química. Nessas reações, átomos e moléculas originais interagem, criando novos átomos e moléculas. No entanto, verificava-se empiricamente que a massa total permanecia a mesma. É neste contexto histórico que foi enunciado o princípio da conservação da massa.

Atualmente, sabemos que nessas reações químicas e interações subatômicas, uma parcela da massa é convertida em outras formas de energia e vice-versa, ou seja, a massa não é uma grandeza conservada. No entanto, como a diferença de massa é uma insignificante parcela da massa total do sistema, balanças e outros equipamentos de laboratório da época não eram capazes de detectá-la.

Com os dados precisos disponíveis atualmente, podemos ter uma ideia da conversão de massa em energia fazendo alguns cálculos que envolvem núcleos atômicos simples. Como exemplo, vamos pegar o deutério, um isótopo do átomo de hidrogênio (possui o mesmo número de prótons do hidrogênio, que é um, mas diferentes números de nêutrons). Além do próton, que constitui o núcleo do hidrogênio, o núcleo do deutério (conhecido como dêuteron), possui também um nêutron, $n$ .

A massa do próton é $m_p = 1,\!00727647u$ e a do nêutron é $m_n = 1,\!008664891u$ , onde $u$ é a chamada unidade de massa atômica e equivale a $1,\!6605402 \times 10^{-27}$ kg.

Somando-se as massas do próton e nêutron, encontramos

$m_p + m_n = 2,\!01594u$

Por outro lado, a massa do dêuteron é

$m_d = 2,\!01355u$

Ou seja, a soma das massas dos constituintes do dêuteron é maior do que a massa do próprio dêuteron:

$m_p+m_n -m_d \approx 0,00239u \quad \Rightarrow \quad m_p+m_n > m_d$

Afinal, para onde vai a diferença de massa? Poderíamos inferir que ela simplesmente desaparece e concluirmos que massa não é uma grandeza conservada em sistemas envolvendo partículas subatômicas.

No entanto, hoje sabemos que essa diferença se encontra na forma de energia de ligação que mantém coesos o próton e o nêutron no núcleo. Ou seja, uma parte da massa passa a se manifestar em forma de energia!

Igualmente fascinante é a massa do próprio próton. De acordo com o chamado modelo de pártons da física de partículas e da cromodinâmica quântica (QCD), o próton não é uma partícula fundamental. Ele é constituído por partículas supostamente fundamentais, os quarks. A distâncias muito pequenas, ele é um objeto bem mais complexo por conta da flutuação do vácuo da mecânica quântica, mas é bem fundamento que dois quarks chamados up (u) e chamado down (d) são os constituintes básicos. É espantoso saber que esses quarks juntos possuem massa total da ordem de 1% da massa do próton!

De onde vem 99% da massa do próton? Da energia de ligação, que no caso trata-se da chamada interação forte.

Para mais detalhes sobre Física das Partículas, sugerimos o site Dinâmica das Interações Fundamentais, da autoria do Prof. Felipe Ponciano de Novaes, acessível aos alunos do ensino médio.

Teoria da relatividade e a equivalência massa-energia

Conforme exemplos acima, é fato consumado que o princípio da conservação de massa, enunciado por Lavoisier e outros, falha. Afirmamos acima que a diferença de massa se transforma em energia de ligação. No entanto, é possível que massa possa se transformar em energia e vice-versa?

Em 1905, Albert Einstein apresentou a sua teoria da relatividade especial. Uma das predições dessa teoria é a famosa fórmula

$E=mc^2 \quad \textrm{(1)}$

que representa a equivalência entre massa e energia. $c$ é a velocidade da luz no vácuo e tem o valor exato 299.792.458 m/s ou aproximadamente $c= 3 \times 10^8$ m/s, e é uma das constantes físicas fundamentais.

Mediante essa equação, é possível que massa possa ser convertida em energia e energia possa ser convertida em massa. Assim, o princípio da conservação de energia continua válida, mas temos que acrescentar a massa como uma nova forma de energia.

Mas a pergunta é: como Einstein concluiu que $E=mc^2$ ?

Vamos focar aqui apenas na equivalência entre massa e energia prevista pela Teoria da Relatividade Especial. Caso queira conhecer melhor a teoria de Einstein indicamos o site Relatividade Restrita, da autoria do Prof. Ricardo Vieira Pereira, que possui uma linguagem acessível a alunos do ensino médio.

No contexto da Mecânica Clássica, discutimos o teorema trabalho-energia cinética (para relembrar, clique no link Trabalho e Forças Conservativas). Relembrando, o trabalho realizado por uma força $F$ resultante sobre um corpo é igual a variação da energia cinética desse corpo, ou seja, $W =\Delta K$ .

Para uma partícula se deslocando em linha reta sob ação de uma força resultante variável ao longo do eixo $x$ , de $x_1$ para $x_2$ , tem-se que

$\Delta K =W = \int_{x_1}^{x_2} F\; dx=\int_{x_1}^{x_2}\frac{dp}{dt}dx$

onde escrevemos a segunda lei de Newton em termos da variação do momento linear, conforme discutido na página Momento linear e sua conservação.

Para dar conta dos efeitos relativísticos, a expressão do momento linear de uma partícula de massa $m$ é modificada para

$\vec{p} = \gamma m \vec{u} \quad \textrm{(2)}$

onde $\vec{u}$ é a velocidade da partícula em relação ao observador e

$\gamma = \frac{1}{\sqrt{1-u^2/c^2}}$

é o chamado fator de Lorentz.

Alguns atribuem a quantidade $\gamma m$ como sendo a massa relativística do objeto e $m$ simplesmente como massa de repouso. Contudo, atualmente essa nomenclatura é ultrapassada. Por massa, entendemos como sendo a quantidade $m$ , que é uma propriedade da partícula e portanto medida no seu referencial de repouso.

Por simplicidade, vamos tomar um movimento retilíneo e utilizar a relação escalar $p=\gamma m u$ . Como $m$ é constante, temos que

$\frac{dp}{dt}=\frac{d}{dt}\left(\frac{mu}{\sqrt{1-\frac{u^2}{c^2}}}\right)=\frac{m}{(1-\frac{u^2}{c^2})^{3/2}}\frac{du}{dt}$

Substituindo a expressão acima na integral e fazendo $dx=udt$ (já que $u = dx/dt$ ), temos uma integral na variável $u$ . Os limites vão de $u_1$ (partícula na posição $x_1$ ) a $u_2$ (partícula na posição $x_2$ ). Para simplificar, vamos tomar $u_1=0$ (portanto $K_1=0$ ) e $u_2=u$ . Então,

$K=m \int_0^u \frac{u}{(1-u^2/c^2)^{3/2}} du = \frac{mc^2}{\sqrt{1-\frac{u^2}{c^2}}}-mc^2$

Reescrevendo a equação acima numa forma mais sugestiva,

$\frac{mc^2}{\sqrt{1-\frac{u^2}{c^2}}} = K + mc^2 \quad \Rightarrow \quad E = K + mc^2$

onde identificamos o termo à esquerda como sendo a energia total da partícula:

$E= mc^2/\sqrt{1-u^2/c^2}= \gamma mc^2 \quad \textrm{(3)}$

Se $K=0$ , ou seja, a partícula se encontra em repouso, temos que

$E = mc^2$

É daí que vem a famosa equação de Einstein; $mc^2$ é identificada como sendo a energia de repouso de uma partícula de massa $m$ . O simples fato da partícula ter massa implica que ela tem energia, mesmo parada!

No limite não relativístico, $u$ é pequeno e portanto $u/c$ é muito menor do que 1. Nesse limite, podemos fazer uma aproximação para o fator de contração de Lorentz utilizando a expansão binomial com expoente negativo, já utilizada na seção Energia Potencial. Neste caso, como $n=1/2$ e $x = -(u/c)^2$ , temos

$\frac{1}{(1-u^2/c^2)^{1/2}} = 1-\frac {1}{2}\left(-\frac{u^2}{c^2}\right)+\ldots \approx 1 + \frac{1}{2}\frac{u^2}{c^2}$

Para $u \ll c$ , as potências $(u/c)^4$ e maiores podem ser ignoradas, pois possuem valores muito pequenos.

Substituindo a aproximação na equação da energia:

$\left(1 + \frac{1}{2}\frac{u^2}{c^2}\right) mc^2 = K + mc^2 \quad \Rightarrow \quad K = \frac{1}{2} mu^2$

ou seja, recuperamos a equação clássica para a energia cinética: $K = mu^2/2$ .

Podemos relacionar a energia total com o momento relacionando as equações

$E=\gamma mc^2 \quad \textrm{ e } \quad p=\gamma mu$

Devemos elevar as duas equações ao quadrado, em seguida multiplicar a equação do momento ao quadrado por $c^2$ e por fim subtrair $E^2$ de $p^2 c^2$ :

$E^{2}-p^2 c^2 =\frac{m^2c^4}{1-\frac{u^2}{c^2}} - \frac{m^2 u^2 c^2}{1-\frac{u^2}{c^2}} = m^2 c^4$

de forma que

$E^2=p^2c^2+m^2c^4 \quad \textrm{(4)}$

Podemos fazer duas observações acerca da equação acima:

Ela mostra que quando o objeto está em repouso, 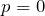$p=0$ , e portanto a energia do sistema é 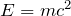$E=mc^2$ . Nada de novo, pois este resultado já foi obtido acima.
A equação permite calcular a energia para partículas que possuem massa nula. No caso, sabemos que o fóton , que é o quanta da onda eletromagnética, é uma partícula fundamental de massa nula. Para o fóton,
$E=pc$

De acordo com a teoria da relatividade, como o fóton possui massa zero, não possui referencial de repouso. Logo, enquanto existir possuirá algum momento diferente de zero e portanto energia diferente de zero também.

Exemplo 1: o decaimento do nêutron

A partir da expressão relativística $E^2 = p^2 c^2 + m^2 c^4$ , onde a massa (multiplicada por $c^2$ ) é considerada energia, podemos entender o que ocorre com a massa quando ela não se conserva. No caso, vamos analisar o decaimento (desintegração) do nêutron livre (condição quando ele está fora de um núcleo atômico). Nesta condição, o nêutron decai segundo o processo

$n \to p + e^- + \bar{\nu}_e$

ou seja, ele desaparece e dá origem a um próton ( $p$ ), um elétron ( $e^-$ ) e um antineutrino do elétron ( $\bar{\nu}_e$ ). Para um maior conhecimento dessas partículas elementares e suas propriedades, sugerimos o site Dinâmica das Interações Fundamentais, criado pelo Prof. Felipe Ponciano de Novaes, que é bem acessível a alunos do ensino médio.

Vamos analisar a massa total antes e depois do decaimento. Para esta finalidade, vamos expressar as massas das partículas em unidade de eV/c $^2$ , onde eV é a unidade conhecida como elétron-volts, onde 1 eV é aproximadamente igual a $1,\!602 \times 10^{-19}$ J. Temos que

$\begin{align*} &\textrm{Massa do n\^eutron}: m_n = 939,\!57 \;\textrm{MeV}/\textrm{c}^2 \\ &\textrm{Massa do pr\'oton}: m_p = 938,\!28 \;\textrm{MeV}/\textrm{c}^2 \\ & \textrm{Massa do el\'etron}: m_e = 0,\!511 \;\textrm{eV}/\textrm{c}^2 \\ & \textrm{Massa do antineutrino do el\'etron}: m_\nu < 2 \;\textrm{eV}/\textrm{c}^2 \end{align*}$

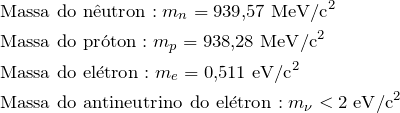
onde MeV (leia-se mega elétron-volts) é $10^6$ eV.

Temos que $m_n = 939,\!57$ MeV/c $^2$ é maior do que a soma das massas do seu produto de decaimento, que dá $m_p+m_e+m_\nu \approx 938,791$ MeV/c $^2$ . O que ocorre com $0,\!779$ MeV/c $^2$ ?

Vamos supor que o nêutron se encontra em repouso. Neste caso, considerando-se que a energia total relativística se conserva no processo de decaimento, tem-se

$E_\textrm{inicial} = E_\textrm{final} \quad \Rightarrow \quad m_n c^2 = m_p c^2 + m_e c^2 + m_\nu c^2 + K_\textrm{total}$

Logo,

$K_\textrm{total} = (m_n -m_p-m_2-m_\nu)c^2$

Ou seja, a diferença de massa vezes $c^2$ se transforma em energia cinética dos produtos de decaimento. De fato, experimentos mostram que o próton, o elétron e o antineutrino do elétron são materializados já em movimento.

Colisões Relativísticas

Assim como numa colisão clássica, o momento linear se conserva numa colisão relativística. No entanto, há três detalhes importantes a observar:

O momento linear da partícula é dada pela Eq. (2)
A energia total é sempre conservada numa colisão relativísitica. Na equação da conservação de energia, não se esquecer da Eq. (1). Massa é energia!
Assim como na colisão clássica, quando a energia cinética total se conserva, estamos falando de uma colisão elástica.
Observa-se no entanto, que essa situação só ocorre quando a massa total se conservar. Basicamente, nessas colisões, as partículas que interagem permanecem as mesmas.

Vale lembrar também que as conservações do momento linear e da energia total ocorrem também em processos de decaimento.

Exemplo 2: o decaimento do píon

O píon ( $\pi$ ), ou méson pi, é uma partícula composta produzida na atmosfera a partir da interação dos raios cósmicos com a atmosfera da Terra.

Para ser mais exato, há três tipos de píons, cuja principal diferença entre eles é a carga elétrica: $\pi^+, \pi^-$ e $\pi^0$ , com cargas iguais a $+e, -e$ e $0$ , onde $e \approx 1,\!6 \times 10^{-19}$ C é a carga elétrica fundamental.

Um $\pi^-$ , logo após ser produzido, decai quase que instantaneamente em um múon ( $\mu$ ) e um neutrino do múon ( $\nu_\mu$ ), na grande maioria das vezes.

Se píon se encontra em repouso, qual a velocidade com que o múon é produzido?

Conforme visto acima, é totalmente razoável desprezarmos a massa do neutrino, pois tanto o píon como o múon possuem massas muito maiores: $m_\pi \approx 140$ MeV/ $c^2$ e $m_\mu \approx 106$ MeV/ $c^2$ , enquanto $m_\nu$ é da ordem de 1 eV/ $c^2$ , no máximo; lembrando que 1 mega (M) é igual a $10^6$ .

Pela conservação do momento linear,

$0 = \vec{p}_\mu + \vec{p}_\nu \quad \Rightarrow \quad p_\mu^2 = p_\nu^2$

Usando $E^2 = p^2 c^2 + m^2 c^4$ para a igualdade acima,

$E_\mu^2 -m_\mu^2 c^4 = E_\nu^2$

Pela conservação de energia, sabendo-se que o píon está em repouso:

$m_\pi c^2 = E_\mu + E_\nu \quad \Rightarrow \quad E_\nu = m_\pi c^2 - E_\mu$

Substituindo $E_\nu$ na penúltima equação acima,

$E_\mu = \frac{m_\pi^2+m_\mu^2}{2m_\pi}c^2$

Podemos determinar o módulo do momento linear do múon usando a relação energia-momento, $E^2 = p^2 c^2 + m^2 c^4$ :

$p_\mu = \sqrt{\frac{E_\mu^2 -m_\mu^2 c^4}{c^2}} \quad \Rightarrow \quad p_\mu = \frac{m_\pi^2-m_\mu^2}{2m_\pi}c$

Vamos escrever as equações (2) e (3), dadas acima, que são respectivamente

$\vec{p} = \gamma m \vec{u} \quad \textrm{ e } \quad E = \gamma m c^2$

Dividindo a primeira pela segunda, obtemos

$\frac{\vec{p}}{E} = \frac{\vec{u}}{c^2}$

Utilizando os dados das massas do píon e do múon, obtemos $u_\muon = 0,\!27 c$ .

Evidentemente, como consideramos $m_\nu=0$ , a sua velocidade será $u_\nu = c$ .

No exemplo 1, consideramos o decaimento do nêutron, dado pelo processo

$n \to p + e^- + \bar{\nu}_e$

Poderíamos ter usado as conservações de energia e momento linear nesse decaimento e obter a velocidade do próton?

Em princípio, sim. No entanto, esse é um processo que envolvem três corpos no estado final. Como há mais variáveis do que equações, a velocidade do próton, assim como a sua energia, não possui um valor único. Se conhecermos os detalhes da interação entre as partículas, podemos determinar o espectro de energia do próton advindo do nêutron.